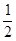题目内容
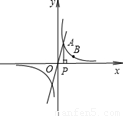
已知正比例函数y=4x的图像与反比例函数y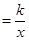 (k≠0)在第一象限的图像交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为
(k≠0)在第一象限的图像交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为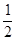
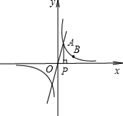
(1)求反比例函数的解析式;
(2)如果点B为反比例函数在第一象限图象上的点(点B与点A不重合),且点B的横坐标为1,在x轴上求一点M,使MA+MB最小。
(1)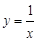 ;(2)(
;(2)(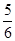 ,0)
,0)
解析试题分析:(1)设A点坐标为(x,y),由题意可知OP=x,PA=y,根据△OAP的面积为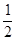 即可求得结果;
即可求得结果;
(2)先根据点B的横坐标是1求得点B的坐标,再根据点A 也在直线y=4x上且点A在第一象限求得点A的坐标,即可得到点A关于x轴对称的点A′的坐标,设直线A′B的解析式为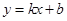 ,把点A′、B的坐标代入即可得到直线
,把点A′、B的坐标代入即可得到直线 的解析式,从而可以求得结果.
的解析式,从而可以求得结果.
(1)设A点坐标为(x,y),由题意可知OP=x,PA=y
∴S△AOP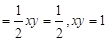
∵点A在反比例函数图象上
∴
∴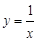 ;
;
(2)∵点B的横坐标是1
∴B(1,1)
∵点A 也在直线y=4x上
∴4x=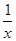 解得x=±
解得x=±
∵点A在第一象限
∴A点的横坐标是
∴点A的坐标( ,2)
,2)
∴点A关于x轴对称的点A′的坐标是( ,-2)
,-2)
设直线A′B的解析式为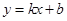 把点A′、B的坐标代入得
把点A′、B的坐标代入得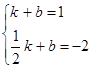 ,解得
,解得
∴直线 的解析式为y="6x-5"
的解析式为y="6x-5"
当y=0时,x=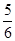 所以点M的坐标为(
所以点M的坐标为(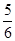 ,0).
,0).
考点:反比例函数的性质,轴对称-最短路线的应用
点评:本题知识点较多,综合性强,难度较大,正确理解轴对称的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

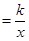 (k≠0)在第一象限的图像交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为
(k≠0)在第一象限的图像交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为