题目内容
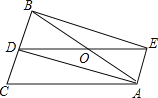
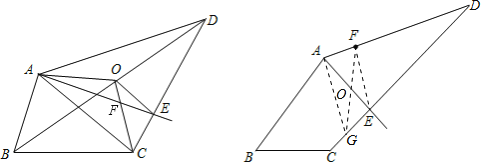
【题目】我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:在四边形ABCD(图2)中,取对角线BD的中点O,连接OA、OC.得折线AOC,再过点O作OE∥AC交CD于E,则直线AE即为四边形ABCD的一条“好线”.
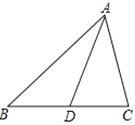
(1)如图,试说明中线AD平分△ABC的面积;
(2)如图,请你探究四边形ABCO的面积和四边形ABCD面积的关系,并说明理由;
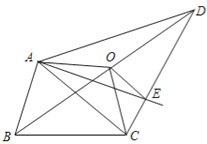
(3)在上图中,请你说明直线AE是四边形ABCD的一条“好线”;
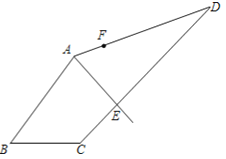
(4)如图,若AE为一条“好线”,F为AD边上的一点,请作出四边形ABCD经过F点的“好线”,并对你的画图作适当说明.
【答案】(1)三角形的一条中线将这个三角形分成面积相等的两个三角形
(2)关系: ![]()
(3)AE是四边形ABCD的一条“好线”.
(4)GF为一条“好线”
【解析】试题分析:(1)![]() ABD和
ABD和![]() ACD是等底同高的两个三角形,故面积相等;(2)由(1)知,S△AOB=S△AOD, S△BOC=S△DOC,故
ACD是等底同高的两个三角形,故面积相等;(2)由(1)知,S△AOB=S△AOD, S△BOC=S△DOC,故![]() (3)设AE与OC的交点是F.要说明直线AE是“好线”,根据已知条件中的折线AOC能平分四边形ABCD的面积,只需说明三角形AOF的面积等于三角形CEF的面积.则根据两条平行线间的距离相等,结合三角形的面积个数可以证明三角形AOE的面积等于三角形COE的面积,再根据等式的性质即可证明;
(3)设AE与OC的交点是F.要说明直线AE是“好线”,根据已知条件中的折线AOC能平分四边形ABCD的面积,只需说明三角形AOF的面积等于三角形CEF的面积.则根据两条平行线间的距离相等,结合三角形的面积个数可以证明三角形AOE的面积等于三角形COE的面积,再根据等式的性质即可证明;
(4)根据两条平行线间的距离相等,只需借助平行线即可作出过点F的“好线”;
试题解析:
(1)在△ABC中,AD是中线,则BD=CD.△ABD和△ADC的底边相等.高相等,都是从A点向BC边所作的垂线段.
由三角形的面积公式, ![]() ,
,
可知三角形的一条中线将这个三角形分成面积相等的两个三角形
(2)关系: ![]()
由(1)知,S△AOB=S△AOD, S△BOC=S△DOC,
∴![]()
∴![]()
(3)∵OE∥AC,
∴ S△AOE=S△COE,
∵S△AOF=S△CEF,
又因为(2)知,折线AOC能平分四边形ABCD的面积,
∴直线AE平分四边形ABCD的面积,即AE是四边形ABCD的一条“好线”.
(4)连接EF,过A作EF的平行线交CD于点G,连接FG,则GF为一条“好线”.
∵AG∥EF,
∴S△AGE=S△AFG.
设AE与FG的交点是O.则S△AOF=S△GOE,
又AE为一条“好线”,所以GF为一条“好线”

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案