��Ŀ����
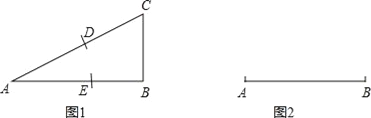
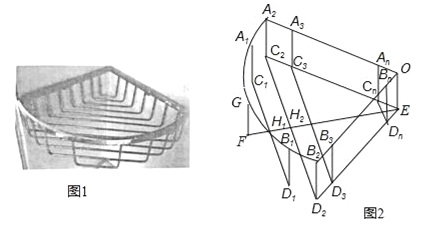
����Ŀ����ͼ1��һ������˿Χ�ɵ���������������һ�����Ƶ�������������ͼ2��������һ���뾶Ϊr��Բ�Ľ�90�������A2OB2������A2C2EO��B2D2EO�������ɸ�ȱһ�ߵľ���״��A1C1D1B1��A2C2D2B2������AnBnCnDn��OEFGΧ�ɣ�����A1��G��B1��![]() �ϣ�A2��A3����An��B2��B3����Bn�ֱ��ڰ뾶OA2��OB2�ϣ�C2��C3������Cn��D2��D3��Dn�ֱ���EC2��ED2�ϣ�EF��C2D2��H2��C1D1��EF��H1��FH1=H1H2=d��C1D1��C2D2��C3D3��CnDn���εȾ���ƽ���ŷţ����һ������״��ı�CnDn���E��ľ���Ӧ������d����A1C1��A2C2��A3C3�Ρ���AnCn��
�ϣ�A2��A3����An��B2��B3����Bn�ֱ��ڰ뾶OA2��OB2�ϣ�C2��C3������Cn��D2��D3��Dn�ֱ���EC2��ED2�ϣ�EF��C2D2��H2��C1D1��EF��H1��FH1=H1H2=d��C1D1��C2D2��C3D3��CnDn���εȾ���ƽ���ŷţ����һ������״��ı�CnDn���E��ľ���Ӧ������d����A1C1��A2C2��A3C3�Ρ���AnCn��
��1����d��ֵ��
��2������CnDn���E��ľ����ܷ����d������ܣ����������n��ֵ��������ܣ���ô����֮��ľ����Ƕ��٣�
���𰸡���1��![]() ����2�����ܣ�
����2�����ܣ�![]() ��
��
��������
�����������1������d=![]() FH2�����EH2���ɽ�����⣮
FH2�����EH2���ɽ�����⣮
��2������CnDn���E��ľ����ܵ���d���г�����n�ķ�����⣬����nû�������⣬��![]() =
=![]() ��4.8�����n���ɽ�����⣮
��4.8�����n���ɽ�����⣮
�����������1����RT��D2EC2�У��ߡ�D2EC2=90�㣬EC2=ED2=r��EF��C2D2����EH1=![]() r��FH1=r��
r��FH1=r��![]() r����d=
r����d=![]() =
=![]() ��
��
��2������CnDn���E��ľ����ܵ���d��������![]() ���������nû�������⣬���Լ��費������
���������nû�������⣬���Լ��費������
��![]() =
=![]() ��4.8����n=6����ʱCnDn���E��ľ���=
��4.8����n=6����ʱCnDn���E��ľ���=![]() =
=![]() ��
��

 ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д� 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�