题目内容
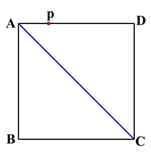
【题目】(1)如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.求证: ![]() .(这个比值
.(这个比值![]() 叫做AE与AB的黄金比.)
叫做AE与AB的黄金比.)
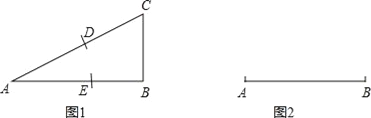
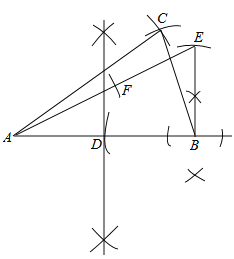
(2)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
(注:直尺没有刻度!作图不要求写作法,但要求保留作图痕迹,并对作图中涉及到的点用字母进行标注)
【答案】(1)证明见解析;(2)作图见解析.
【解析】试题分析:(1)利用位置数表示出AB,AC,BC的长,进而得出AE的长,进而得出答案.
(2)根据底与腰之比均为黄金比的等腰三角形,画图即可.
试题解析:解:(1)证明:∵Rt△ABC中,∠B=90°,AB=2BC,
∴设AB=2x,BC=x,则AC= ![]() .
.
∴AD=AE= ![]() .∴
.∴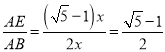 .
.
(2)底与腰之比均为黄金比的等腰三角形,如答图,△ABC即为所求.

练习册系列答案
相关题目