��Ŀ����
����Ŀ���Ķ����⣺
��ͼ�٣�����ı���ABCD����AB=AD��CB=CD����B=��D=90�㣬��ô���ǰ��������ı��ν������������Ρ���
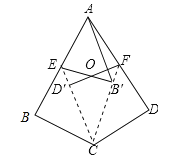
��һ����ͼ����ʾ�ġ��������Ρ�ֽƬABCD���۵�����ͼ����ʾ��״����չ���õ�ͼ�ۣ�����CE��CFΪ�ۺۣ���BCE=��ECF=��FCD����B��Ϊ��B�Ķ�Ӧ�㣬��D��Ϊ��D�Ķ�Ӧ�㣬����EB�䣬FD���ཻ�ڵ�O��

��Ӧ�ã�
��1����ƽ���ı��Ρ����Ρ����Ρ�����������ͼ���У�һ��Ϊ���������Ρ����� ��
��2����ͼ���еġ�BCD=120��ʱ����AEB��= �㣻
��3����ͼ���е��ı���AECFΪ����ʱ����Ӧͼ���еġ��������Ρ��� ���������ı���ABCD����
��չ������
��4����ͼ���еġ�BCD=90��ʱ������AB�䣬��̽���AB��E�Ķ�������˵�����ɣ�
���𰸡���1������������2��80����3��5����4��45�㣮
��������
�����������1�����ƽ���ı��Ρ����Ρ����Ρ������ε����ʺ͡��������Ρ��Ķ��������ó����ۣ�
��2����֤��AEB��=��BCB�䣬��������BCE=��ECF=40�㣬���ɵó������
��3�����۵������ʵó�BE=B��E��BC=B��C����B=��CB��E=90�㣬CD=CD�䣬FD=FD�䣬��D=��CD��F=90�㣬���ɵó��ı���EBCB�䡢�ı���FDCD���ǡ��������Ρ���������ó���OD��E=��OB��F=90�㣬CD��=CB�䣬�����ε����ʵó�AE=AF��CE=CF����֤����OED���ա�OFB�䣬�ó�OD��=OB�䣬OE=OF��֤����AEB��=��AFD��=90�㣬���ɵó��ı���CD��OB�䡢�ı���AEOF�ǡ��������Ρ������ɵó����ۣ�
��4����ͼ���е���BCD=90��ʱ���ı���ABCD�������Σ�֤��A��E��B�䡢F�ĵ㹲Բ������![]() ����Բ�ܽǶ������ɵ�����AB��E�Ķ�����
����Բ�ܽǶ������ɵ�����AB��E�Ķ�����
�����������1�������ı���ABCD��ƽ���ı��Σ���AB=CD��AD=BC����A=��C��90�㣬��B=��D��90�㣬��AB��AD��BC��CD����ƽ���ı��β�һ��Ϊ���������Ρ���
�����ı���ABCD�Ǿ��Σ����A=��B=��C=��D=90�㣬AB=CD��AD=BC����AB��AD��BC��CD�������β�һ��Ϊ���������Ρ���
�����ı���ABCD�����Σ���AB=BC=CD=AD����A=��C��90�㣬��B=��D��90�㣬�����β�һ��Ϊ���������Ρ���
�����ı���ABCD�������Σ����A=��B=��C=��D=90�㣬AB=BC=CD=AD����������һ��Ϊ���������Ρ���
����ƽ���ı��Ρ����Ρ����Ρ�����������ͼ���У�һ��Ϊ���������Ρ����������Σ��ʴ�Ϊ�������Σ�
��2����������ã���B��=��B=90�㣬�����ı���CBEB���У���BEB��+��BCB��=180�㣬�ߡ�AEB��+��BEB��=180�㣬���AEB��=��BCB�䣬�ߡ�BCE=��ECF=��FCD����BCD=120�㣬���BCE=��ECF=40�㣬���AEB��=��BCB��=40��+40��=80�㣻�ʴ�Ϊ��80��
��3����ͼ���е��ı���AECFΪ����ʱ����Ӧͼ���еġ��������Ρ���5�����������£�
��������ã�BE=B��E��BC=B��C����B=��CB��E=90�㣬CD=CD�䣬FD=FD�䣬��D=��CD��F=90�㣬���ı���EBCB�䡢�ı���FDCD���ǡ��������Ρ���
���ı���ABCD�ǡ��������Ρ�����AB=AD��CB=CD����B=��D=90�㣬��CD��=CB�䣬��CD��O=��CB��O=90�㣬���OD��E=��OB��F=90�㣬���ı���AECFΪ���Σ���AE=AF��CE=CF��AE��CF��AF��CE����D��E=B��F����AEB��=��CB��E=90�㣬��AFD��=��CD��F=90�㣬����OED�����OFB���У��ߡ�OD��E=��OB��F����EOD��=��FOB����D��E=B��F�����OED���ա�OFB�䣨AAS������OD��=OB�䣬OE=OF�����ı���CD��OB�䡢�ı���AEOF�ǡ��������Ρ���
�������ı���ABCD����Ӧͼ���еġ��������Ρ���5�����ʴ�Ϊ��5��
��4����ͼ���е���BCD=90��ʱ����ͼ��ʾ���ı���ABCD�������Σ����A=90�㣬�ߡ�EB��F=90�㣬���A+��EB��F=180�㣬��A��E��B�䡢F�ĵ㹲Բ����AE=AF����![]() �����AB��E=��AB��F=
�����AB��E=��AB��F=![]() ��EB��F=45�㣮
��EB��F=45�㣮