题目内容
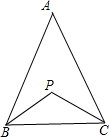
已知△ABC,(1)如图,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+| 1 |
| 2 |
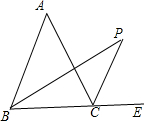
(2)如图,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;
(3)如图,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
| 1 |
| 2 |
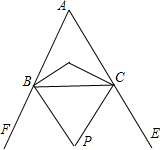
其中结论一定正确的序号数是
分析:根据三角形的内角和外角之间的关系计算.
解答:解:(1)∵若P点是∠ABC和∠ACB的角平分线的交点,
∴∠ABP=∠PBC,∠ACP=∠PCB
∵∠A=180°-∠ABC-∠ACB=180°-2(∠PBC+∠PCB)
∠P=180°-(∠PBC+∠PCB)
∴∠P=90°+
∠A;
故(1)的结论正确;
(2)∵∠A=∠ACE-∠ABC=2∠PCE-2∠PBC=2(∠PCE-∠PBC)
∠P=∠PCE-∠PBC
∴2∠P=∠A
 故(2)的结论是错误.
故(2)的结论是错误.
(3)∠P=180°-(∠PBC+∠PCB)
=180°-
(∠FBC+∠ECB)
=180°-
(∠A+∠ACB+∠A+∠ABC)
=180°-
(∠A+180°)
=90°-
∠A.
故(3)的结论正确.
故答案为:(1)(3).
∴∠ABP=∠PBC,∠ACP=∠PCB
∵∠A=180°-∠ABC-∠ACB=180°-2(∠PBC+∠PCB)
∠P=180°-(∠PBC+∠PCB)
∴∠P=90°+
| 1 |
| 2 |
故(1)的结论正确;
(2)∵∠A=∠ACE-∠ABC=2∠PCE-2∠PBC=2(∠PCE-∠PBC)
∠P=∠PCE-∠PBC
∴2∠P=∠A
 故(2)的结论是错误.
故(2)的结论是错误.(3)∠P=180°-(∠PBC+∠PCB)
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
故(3)的结论正确.
故答案为:(1)(3).
点评:主要考查了三角形的内角和外角之间的关系.
(1)三角形的外角等于与它不相邻的两个内角和;
(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.
(1)三角形的外角等于与它不相邻的两个内角和;
(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
已知ABC的三边满足a2+b2+c2-ab-bc-ac=0,则这个三角形的形状是( )
| A、直角三角形 | B、等腰三角形 | C、等腰直角三角形 | D、等边三角形 |
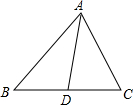 如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )
如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )| A、3<AD<4 | ||||
| B、1<AD<7 | ||||
C、
| ||||
D、
|
已知△ABC中,cosA=
,tgB=1,则△ABC的形状是( )
| 1 |
| 2 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
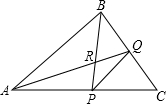 如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于
如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于