题目内容
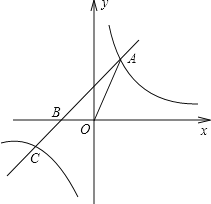
【题目】如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=(m+5)x2m+1交于点A、C,其中点A在第一象限,点C在第三象限.
(1)求双曲线的解析式;
(2)求B点的坐标;
(3)若S△AOB=2,求A点的坐标;
(4)在(3)的条件下,在x轴上是否存在点P,使△AOP是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)B(﹣2,0)(3)A(2,2)(4)P1(2,0),P2(4,0),P3(﹣2
(2)B(﹣2,0)(3)A(2,2)(4)P1(2,0),P2(4,0),P3(﹣2![]() ,0),P4(2
,0),P4(2![]() ,0)
,0)
【解析】
试题分析:(1)根据双曲线函数的定义可以确定m的值;
(2)利用y=kx+2k当y=0时,x=2就知道B的坐标;
(3)根据(1)知道OB=2,而S△AOB=2,利用它们可以求出A的坐标;
(4)存在点P,使△AOP是等腰三角形.只是确定P坐标时,题目没有说明谁是腰,是底,所以要分类讨论,不要漏解.
解:(1)∵y=(m+5)x2m+1是双曲线
∴![]() .
.
∴m=﹣1(2分)
∴![]() (3分)
(3分)
(2)∵直线y=kx+2k(k≠0)与x轴交于点B
∴当y=0时,0=kx+2k
∴x=﹣2(5分)
∴B(﹣2,0)(6分)
(3)∵B(﹣2,0)
∴OB=2(7分)
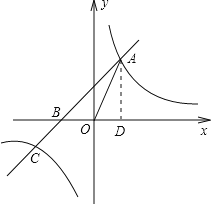
过A作AD⊥x轴于点D
∵点A在双曲线y=![]() 上,
上,
∴设A(a,b)
∴ab=4,AD=b(8分)
又∵S△AOB=![]() OBAD=
OBAD=![]() ×2b=2
×2b=2
∴b=2(9分)
∴a=2,
∴A(2,2)(10分)
(4)P1(2,0),P2(4,0),P3(﹣2![]() ,0),P4(2
,0),P4(2![]() ,0).
,0).
(写对一个得一分)(14分)

练习册系列答案
相关题目