Question

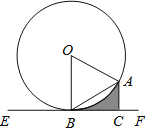
【题目】如图，梯形ABCD中, AD// BC, ∠B=90°, AD=2, BC=5,E是AB上一点，将△BCE沿着直线CE翻折,点B恰好与点D重合,则BE=__

Answer 1

【答案】

【解析】

如图作DM⊥BC于M，先证明四边形ABMD是矩形，在Rt△DMC中求出DM，再在Rt△AED中利用勾股定理即可解决问题．

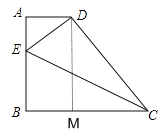
解：如图，作DM⊥BC于M．

∵∠A＝∠B＝∠DMB＝90°，

∴四边形ABMD是矩形，

∴AD＝BM＝2，AB＝DM，

∵点B恰好与点D重合，

∵BC＝CD＝5，

在Rt△DMC中，CM＝BCBM＝3，CD＝5，

∴DM＝AB＝＝4，

设BE＝DE＝x，

在Rt△AED中，∵AE2＋AD2＝ED2，

∴（4x）2＋22＝x2，

解得x＝，即BE＝，

故答案为：．