ЬтФПФкШн
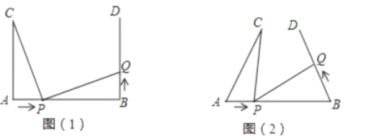
ЁОЬтФПЁПНкШеРяЃЌажЕмСНШЫдк60УзЕФХмЕРЩЯНјааЖЬОрРыБШШќЃЌСНШЫДгГіЗЂЕуЭЌЪБЦ№ХмЃЌИчИчЕНДяжеЕуЪБЃЌЕмЕмРыжеЕуЛЙВю12УзЃЎ
(1)ШєИчИчЕФЫйЖШЮЊ10Уз/УыЃЌ
ЂйЧѓЕмЕмЕФЫйЖШЃЛ
ЂкШчЙћСНШЫжиаТПЊЪМБШШќЃЌИчИчДгЦ№ЕуЯђКѓЭЫ10УзЃЌажЕмЭЌЪБЦ№ХмЃЌСНШЫФмЗёЭЌЪБЕНДяжеЕуЃПШєФмЃЌЧыЧѓГіСНШЫЕНДяжеЕуЕФЪБМфЃЛШєВЛФмЃЌЧыЫЕУїЫЯШЕНДяжеЕуЃЎ
(2)ШєИчИчЕФЫйЖШЮЊmУз/УыЃЌ
ЂйЕмЕмЕФЫйЖШЮЊ________Уз/Уы(гУКЌmЕФДњЪ§ЪНБэЪО)ЃЛ
ЂкШчЙћСНШЫЯыЭЌЪБЕНДяжеЕуЃЌИчИчгІЯђКѓЭЫЖрЩйУзЃП
ЁОД№АИЁПЃЈ1ЃЉЂйЕмЕмЕФЫйЖШЪЧ8Уз/УыЃЛЂкВЛФмЭЌЪБЕНДяЃЌИчИчЯШЕНДяжеЕуЃЛЃЈ2ЃЉЂй0.8mЃЛЂкШчЙћСНШЫЯыЭЌЪБЕНДяжеЕуЃЌИчИчгІЯђКѓЭЫ15Уз
ЁОНтЮіЁП
(1)ЂйИљОнЪБМф=ТЗГЬ![]() ЫйЖШ, МАИчИчХм60УзЕФЪБМф=ЕмЕмХмЃЈ60-12ЃЉУзЕФЪБМфСаГіЗНГЬЃЌЧѓНтМДПЩЃЛ
ЫйЖШ, МАИчИчХм60УзЕФЪБМф=ЕмЕмХмЃЈ60-12ЃЉУзЕФЪБМфСаГіЗНГЬЃЌЧѓНтМДПЩЃЛ
ЂкРћгУЪБМф=ТЗГЬ![]() ЫйЖШЃЌПЩЗжБ№ЧѓГіИчИчЁЂЕмЕмЕНДяжеЕуЕФЪБМфЃЌБШНЯКѓМДПЩЕУГіНсТл;
ЫйЖШЃЌПЩЗжБ№ЧѓГіИчИчЁЂЕмЕмЕНДяжеЕуЕФЪБМфЃЌБШНЯКѓМДПЩЕУГіНсТл;
(2)ЂйИљОнЪБМф=ТЗГЬ![]() ЫйЖШ, МАИчИчХм60УзЕФЪБМф=ЕмЕмХмЃЈ60-12ЃЉУзЕФЪБМф;
ЫйЖШ, МАИчИчХм60УзЕФЪБМф=ЕмЕмХмЃЈ60-12ЃЉУзЕФЪБМф;
ЂкЩшИчИчКѓЭЫyУзЃЌИљОнЪБМф=ТЗГЬ![]() ЫйЖШЃЌМАИчИчХмЃЈ60+yЃЉУзЕФЪБМф=ЕмЕмХм60УзЕФЪБМфСаГіЗНГЬЃЌМДПЩЕУГіЙигкyЕФЗжЪНЗНГЬ,НтжЎОМьбщКѓМДПЩЕУГіНсТл.
ЫйЖШЃЌМАИчИчХмЃЈ60+yЃЉУзЕФЪБМф=ЕмЕмХм60УзЕФЪБМфСаГіЗНГЬЃЌМДПЩЕУГіЙигкyЕФЗжЪНЗНГЬ,НтжЎОМьбщКѓМДПЩЕУГіНсТл.
ЃЈ1ЃЉЂйЩшЕмЕмЕФЫйЖШЮЊxУз/УыЃЌдђ![]()
НтЕУЃКx=8ЃЌ
ОМьбщЃЌx=8ЪЧдЗжЪНЗНГЬЕФНтЃЌЧвЗћКЯЬтвт
Д№ЃКЕмЕмЕФЫйЖШЪЧ8Уз/УыЃЛ
ЂкИчИчХмЭъШЋГЬЫљашвЊЕФЪБМфЮЊ(60+10)ЁТ10=7 (Уы)ЃЌ
ЕмЕмХмЭъШЋГЬЫљашвЊЕФЪБМфЮЊ![]() (Уы)>7УыЃЌ
(Уы)>7УыЃЌ
ЁрИчИчЯШЕНДяжеЕуЃЛ
(2)ЂйЩшЕмЕмЕФЫйЖШЮЊxУз/УыЃЌдђ![]()
НтЕУЃК![]()
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЂкЩшИчИчКѓЭЫyУзЃЌгЩЬтвтЕУЃК![]()
Ёр ![]()
Ёр![]()
Ёрy=15
Д№ЃКШчЙћСНШЫЯыЭЌЪБЕНДяжеЕуЃЌИчИчгІЯђКѓЭЫ15УзЃЎ

 ЛЦИдЙкОќПЮПЮСЗЯЕСаД№АИ
ЛЦИдЙкОќПЮПЮСЗЯЕСаД№АИ