题目内容
已知定点F(0,-2),动点P(x,y)到F点的距离与它到x轴的距离相等.
(1)写出y关于x的函数关系式;
(2)若(1)中的函数图象与过F点的直线y=kx+b交于A、B两点,
ⅰ请用k表示线段AB的长;
ⅱ以AB为弦的圆与y轴交于M(0,-4+2 )、N(0,-4-2
)、N(0,-4-2 )两点,求此时直线y=kx+b的解析式.
)两点,求此时直线y=kx+b的解析式.
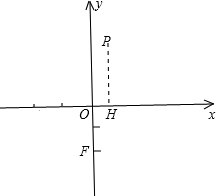 解:(1)过P作PH⊥x轴于H,则PF=P.
解:(1)过P作PH⊥x轴于H,则PF=P.∴
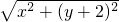 =|y|
=|y|∴y=-
 x2-1;(5分)
x2-1;(5分)(2)ⅰ设A(x1,y1),B(x2,y2)(这里y1<0,y2<0)
∵直线过F(0,-2)
∴直线为y=kx-2
由
 得y2+4(1+k2)y+4(k2+1)=0(6分)
得y2+4(1+k2)y+4(k2+1)=0(6分)A、B在抛物线上,由已知条件知:AB=AF+FB
∴AB=|y1|+|y2|=-(y1+y2)=4(k2+1)(10分)
ⅱ由相交弦定理
AF•FB=FM•FN(11分)
又∵AF•FB=|y1y2|
∴4(k2+1)=8(12分)
∴k=±1
即直线方程为y=±x-2.(13分)
分析:(1)过P作PH⊥x轴于H,则PF=PH,然后表示出PF和PH得到
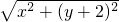 =|y|,两边平方即可得到y与x之间的函数关系式;
=|y|,两边平方即可得到y与x之间的函数关系式;(2)设A(x1,y1),B(x2,y2)(这里y1<0,y2<0),根据直线过F(0,-2),设出直线解析式为y=kx-2,与求得的函数关系式联立即可得到y2+4(1+k2)y+4(k2+1)=0,再根据AB=AF+FB即可表示出AB.
点评:本题考查了一次函数的综合知识,解题的关键是用点的坐标表示出线段的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,下列方格图是由边长为1的小正方形组成的,其中O为一已知定点,
如图,下列方格图是由边长为1的小正方形组成的,其中O为一已知定点,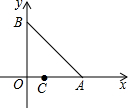 如图,平面直角坐标系xOy中,已知定点A(1,0)和B(0,1),若动点C在x轴上运动,则使△ABC为等腰三角形的点C有( )个.
如图,平面直角坐标系xOy中,已知定点A(1,0)和B(0,1),若动点C在x轴上运动,则使△ABC为等腰三角形的点C有( )个.