题目内容
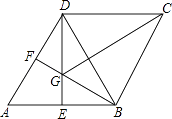
【题目】(1)如图①,△ABC是锐角三角形,高BD,CE相交于点H.找出∠BHC和∠A之间存在何种等量关系;
(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD,CE所在的直线相交于点H,把图②补充完整,并指出此时(1)中的等量关系是否仍然成立?
【答案】 (1)∠A+∠BHC=180° (2)仍然成立
【解析】
(1)根据对顶角的性质,可得∠BHC与∠EHD的关系,根据四边形的内角和定理,可得答案;
(2)根据对顶角的性质,可得∠BHC与∠EHD的关系,根据四边形的内角和定理,可得答案.
(1)由∠BHC与∠EHD是对顶角,得:
∠BHC=∠EHD,
由高BD、CE相交于点H,得:
∠ADH=∠AEH=90°,
由四边形内角和定理,得:
∠A+∠AEH+∠EHD+∠HDA=360°,
∠A+∠EHD=360°-∠AEH-∠HDA=360°-90°-90°=180°,
∴∠BHC+∠A=180°;
(2)由∠BHC与∠EHD是对顶角,得:
∠BHC=∠EHD,
由高BD、CE相交于点H,得:
∠ADH=∠AEH=90°,
由四边形内角和定理,得:
∠H+∠AEH+∠EHD+∠HDA=360°,
∠H+∠DAE=360°-∠AEH-∠HDA=360°-90°-90°=180°,
∴∠BHC+∠BAC=180°.

练习册系列答案
相关题目