题目内容
【题目】如图,在□ABCD中, AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA'E',连接DA',若∠ADC=60°,∠ADA'=50°,则∠DA'E'的大小为( )
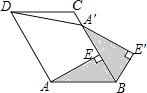
A. 130° B. 150° C. 160° D. 170°
【答案】C
【解析】根据平行四边形对角相等、邻角互补,得∠ABC=60°,∠DCB=120°,再由∠A′DC=10°,可运用三角形外角求出∠DA′B=130°,再根据旋转的性质得到∠BA′E′=∠BAE=30°,从而得到答案.
解:∵四边形ABCD是平行四边形,∠ADC=60°,
∴∠ABC=60°,∠DCB=120°,
∵∠ADA′=50°,
∴∠A′DC=10°,
∴∠DA′B=130°,
∵AE⊥BC于点E,
∴∠BAE=30°,
∵△BAE顺时针旋转,得到△BA′E′,
∴∠BA′E′=∠BAE=30°,
∴∠DA′E′=∠DA′B+∠BA′E′=160°.
故选C.

练习册系列答案
相关题目