��Ŀ����
����Ŀ���ڼס�������ͬѧ��ѡ��һ�˲μӡ��л���ʫ�ʡ�����������ͬ�IJ��������£�����5�β��Գɼ�����λ���֣����£�
�ף�79��86��82��85��83
�ң�88��79��90��81��72��
�ش��������⣺
��1���׳ɼ���ƽ������ ���ҳɼ���ƽ������ ��
��2��������֪![]() =6��
=6��![]() =42������Ϊѡ��˭�μӱ��������ʣ�˵�����ɣ�
=42������Ϊѡ��˭�μӱ��������ʣ�˵�����ɣ�
��3������Ӽס�������5�εijɼ��и������ȡһ�γɼ����з�������鵽�������˵ijɼ�������80�ֵĸ�����
���𰸡���1��83��82����2���ף���3��![]() ��
��
��������
�����������1������ƽ�����Ķ������ʽ���㣻
��2����ƽ��������ʾ��ƽ��ˮƽ�������������ijɼ��ȶ����жϿ�֪��
��3���б���ʾ�����еȿ��ܵĽ�����ҵ���ʹ���¼������Ľ���������ݸ��ʹ�ʽ����ɵã�
�����������1��![]() =��79+86+82+85+83����5=83���֣���
=��79+86+82+85+83����5=83���֣���![]() =��88+79+90+81+72����5=82���֣���
=��88+79+90+81+72����5=82���֣���
��2��ѡ�μײμӱ��������ʣ��������£�
��![]() ��
��![]() ����
����![]() ��
��![]() �����ƽ���ɼ������ң��Ҽijɼ����ȶ�����ѡ�μײμӱ��������ʣ�
�����ƽ���ɼ������ң��Ҽijɼ����ȶ�����ѡ�μײμӱ��������ʣ�
��3���б����£�
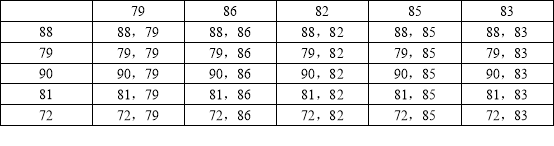
�ɱ����֪�����еȿ��ܽ������25�֣����������˵ijɼ�������80����12�֣���鵽�������˵ijɼ�������80�ֵĸ���Ϊ![]() ��
��

 ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�