��Ŀ����
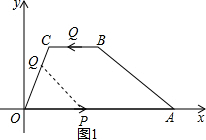
 ��2013•�Ƹԣ���ͼ����ƽ��ֱ������ϵ�У��ı���ABCD�����Σ�����A��6��0����B��3��
��2013•�Ƹԣ���ͼ����ƽ��ֱ������ϵ�У��ı���ABCD�����Σ�����A��6��0����B��3��| 3 |
| 3 |
��1����A��B��C����������ߵĽ���ʽ��
��2������Q��CO�����˶�ʱ�����OPQ�����S��ʱ��t�ĺ�����ϵʽ��
��3����O��P��Q������������ܹ���ֱ�������������ܣ������t��ֵ�������ܣ���˵�����ɣ�
��4������A��B��C����������ߵĶԳ��ᡢֱ��OB��PQ�ܹ�����һ�������ܣ��������ʱt��ֵ����Χ���������ܣ���˵�����ɣ���
��������1�����ô���ϵ����������κ�������ʽ���ɣ�
��2��������֪�ó���OPQ�ĸߣ��������������������ʽ������ɣ�
��3����������ó���0��t��3����0��t��2ʱ��Q��BC�����˶����ó�����OPQΪֱ�������Σ�ֻ���ǡ�OPQ=90����OQP=90�㣬��2��t��3ʱ��Q��OC�����˶����ó���OPQ������Ϊֱ�������Σ�
��4��������������߶Գ����Լ�OBֱ�߽���ʽ��PM�Ľ���ʽ���ó�
��1-t����
=3-t-2t�����������0��t��2ʱ��P��M��Q����һ��ֱ���ϣ�������2��t��3ʱ�����t��ֵ������t��ȡֵ��Χ�ó��𰸣�
��2��������֪�ó���OPQ�ĸߣ��������������������ʽ������ɣ�
��3����������ó���0��t��3����0��t��2ʱ��Q��BC�����˶����ó�����OPQΪֱ�������Σ�ֻ���ǡ�OPQ=90����OQP=90�㣬��2��t��3ʱ��Q��OC�����˶����ó���OPQ������Ϊֱ�������Σ�
��4��������������߶Գ����Լ�OBֱ�߽���ʽ��PM�Ľ���ʽ���ó�
| 3 |
| 3 |
����⣺��1�������������ߵĽ���ʽΪy=ax2+bx+c����A��6��0����B��3��
����C��1��
�������������ã�
��
��ã�
��
�����������߽���ʽΪ��y=-
x2+
x+
��
��2����ͼ1����������ó���OC=CB=2����COA=60�㣬
�൱����Q�˶���OC��ʱ��OQ=4-t��
���OPQ�ĸ�Ϊ��OQ��sin60��=��4-t����
��
�֡�OP=2t��
��S=
��2t����4-t����
=-
��t2-4t����2��t��3����
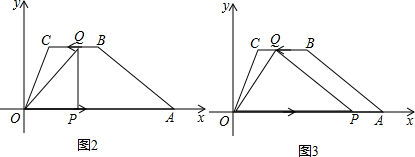
��3�����������0��t��3��
��0��t��2ʱ��Q��BC�����˶�����ʱOP=2t��OQ=
��
PQ=
=
��
�ߡ�POQ����POC=60�㣬
������OPQΪֱ�������Σ�ֻ���ǡ�OPQ=90����OQP=90�㣬
����OPQ=90�㣬��ͼ2����OP2+PQ2=QO2����4t2+3+��3t-3��2=3+��3-t��2��
��ã�t1=1��t2=0����ȥ����
����OPQΪֱ�������Σ�ֻ���ǡ�OPQ=90����OQP=90�㣬
����OQP=90�㣬��ͼ��3����OQ2+PQ2=PO2������3-t��2+6+��3t-3��2=4t2��
��ã�t=2��
��2��t��3ʱ��Q��OC�����˶�����ʱOP=2t��4��
��POQ=��COP=60�㣬
OQ��OC=2��
�ʡ�OPQ������Ϊֱ�������Σ�
������������t=1��t=2ʱ����OPQΪֱ�������Σ�
��4���ɣ�1����֪��������y=-
x2+
x+
=-
��x-2��2+
��
��Գ���Ϊx=2��
�֡�OB��ֱ�߷���Ϊy=
x��
�������߶Գ�����OB����ΪM��2��
����
�֡�P��2t��0��
���P��M��ֱ�߽���ʽΪ��y=kx+b��
��
��
��ã�
��
��ֱ��PM�Ľ���ʽΪ��y=
x-
��
��
��1-t��y=x-2t��
��0��t��2ʱ��Q��3-t��
����������ʽ���ã�
��1-t����
=3-t-2t���������
��0��t��2ʱ��P��M��Q����һ��ֱ���ϣ�
��M��ֱ��PQ�ϣ�
��2��t��3ʱ��OQ=4-t����QOP=60�㣬
��Q��
��
����
������ʽ�ã�
��
��1-t��=
-2t��
��ã�t=2��t=
�����������⣬��ȥ����
��������������֪����A��B��C����������ߵĶԳ���OB��PQ�ܹ�����һ�㣬��ʱ0��t��2��
| 3 |
| 3 |
|
��ã�
|

�����������߽���ʽΪ��y=-
| ||
| 15 |
4
| ||
| 15 |
4
| ||
| 5 |
��2����ͼ1����������ó���OC=CB=2����COA=60�㣬
�൱����Q�˶���OC��ʱ��OQ=4-t��
���OPQ�ĸ�Ϊ��OQ��sin60��=��4-t����
| ||
| 2 |
�֡�OP=2t��
��S=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
��3�����������0��t��3��
��0��t��2ʱ��Q��BC�����˶�����ʱOP=2t��OQ=
| 3+(3-t)2 |

PQ=
| 3+[2t-(3-t)]2 |
| 3+(3t-3)2 |
�ߡ�POQ����POC=60�㣬
������OPQΪֱ�������Σ�ֻ���ǡ�OPQ=90����OQP=90�㣬
����OPQ=90�㣬��ͼ2����OP2+PQ2=QO2����4t2+3+��3t-3��2=3+��3-t��2��
��ã�t1=1��t2=0����ȥ����
����OPQΪֱ�������Σ�ֻ���ǡ�OPQ=90����OQP=90�㣬
����OQP=90�㣬��ͼ��3����OQ2+PQ2=PO2������3-t��2+6+��3t-3��2=4t2��
��ã�t=2��
��2��t��3ʱ��Q��OC�����˶�����ʱOP=2t��4��
��POQ=��COP=60�㣬
OQ��OC=2��
�ʡ�OPQ������Ϊֱ�������Σ�
������������t=1��t=2ʱ����OPQΪֱ�������Σ�
��4���ɣ�1����֪��������y=-
| ||
| 15 |
4
| ||
| 15 |
4
| ||
| 5 |
| ||
| 15 |
16
| ||
| 15 |
��Գ���Ϊx=2��
�֡�OB��ֱ�߷���Ϊy=
| ||
| 3 |
�������߶Գ�����OB����ΪM��2��
2
| ||
| 3 |
�֡�P��2t��0��
���P��M��ֱ�߽���ʽΪ��y=kx+b��
��
|
��ã�
|
��ֱ��PM�Ľ���ʽΪ��y=
| ||
| 3(1-t) |
2
| ||
| 3(1-t) |
��
| 3 |
��0��t��2ʱ��Q��3-t��
| 3 |
| 3 |
| 3 |
��0��t��2ʱ��P��M��Q����һ��ֱ���ϣ�
��M��ֱ��PQ�ϣ�
��2��t��3ʱ��OQ=4-t����QOP=60�㣬
��Q��
| 4-t |
| 2 |
| ||
| 2 |
������ʽ�ã�
| ||
| 2 |
| 3 |
| 4-t |
| 2 |
��ã�t=2��t=
| 4 |
| 3 |
��������������֪����A��B��C����������ߵĶԳ���OB��PQ�ܹ�����һ�㣬��ʱ0��t��2��
������������Ҫ�����˶��κ������ۺ�Ӧ���Լ�����ϵ��������κ�������ʽ�ʹ���ϵ������һ�κ�������ʽ��֪ʶ�����÷�������˼��ó�t��ֵ�ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ

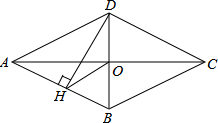 ��2013•�Ƹԣ���ͼ���ı���ABCD�����Σ��Խ���AC��BD�ཻ�ڵ�O��DH��AB��H������OH����֤����DHO=��DCO��
��2013•�Ƹԣ���ͼ���ı���ABCD�����Σ��Խ���AC��BD�ཻ�ڵ�O��DH��AB��H������OH����֤����DHO=��DCO��
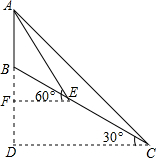 ��2013•�Ƹԣ���ͼ��Сɽ������һ�ź���AB��ɽ��BC�����Ϊ30�㣬��Ϊ�˲�������AB��������Աѡ��ɽ��C��Ϊһ�����㣬�����������Ϊ45�㣬Ȼ��˳ɽ����������100����E�����ٲ����������Ϊ60�㣬������AB���������������
��2013•�Ƹԣ���ͼ��Сɽ������һ�ź���AB��ɽ��BC�����Ϊ30�㣬��Ϊ�˲�������AB��������Աѡ��ɽ��C��Ϊһ�����㣬�����������Ϊ45�㣬Ȼ��˳ɽ����������100����E�����ٲ����������Ϊ60�㣬������AB���������������