题目内容
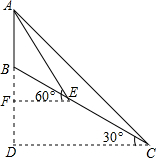（2013•黄冈）如图，小山顶上有一信号塔AB，山坡BC的倾角为30°，现为了测量塔高AB，测量人员选择山脚C处为一测量点，测得塔顶仰角为45°，然后顺山坡向上行走100米到达E处，再测得塔顶仰角为60°，求塔高AB（结果保留整数，| 3 |
| 2 |
分析：先判断△ACE为等腰三角形，在Rt△AEF中表示出EF、AF，在Rt△BEF中求出BF，根据AB=AF-BF即可得出答案．
解答：解：依题意可得：∠AEB=30°，∠ACE=15°，
又∵∠AEB=∠ACE+∠CAE
∴∠CAE=15°，
即△ACE为等腰三角形，
∴AE=CE=100m，
在Rt△AEF中，∠AEF=60°，
∴EF=AEcos60°=50m，AF=AEsin60°=50
m，
在Rt△BEF中，∠BEF=30°，
∴BF=EFtan30°=50×
=
m，
∴AB=AF-BF=50
-
=
≈58（米）．
答：塔高AB大约为58米．
又∵∠AEB=∠ACE+∠CAE
∴∠CAE=15°，
即△ACE为等腰三角形，
∴AE=CE=100m，
在Rt△AEF中，∠AEF=60°，
∴EF=AEcos60°=50m，AF=AEsin60°=50
| 3 |
在Rt△BEF中，∠BEF=30°，
∴BF=EFtan30°=50×
| ||
| 3 |
50
| ||
| 3 |
∴AB=AF-BF=50
| 3 |
50
| ||
| 3 |
100
| ||
| 3 |
答：塔高AB大约为58米．
点评：本题考查了解直角三角形的知识，解答本题的关键是构造直角三角形，利用三角函数表示出相关线段的长度，难度一般．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
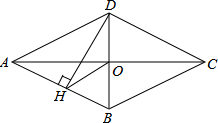（2013•黄冈）如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH，求证：∠DHO=∠DCO．
（2013•黄冈）如图，在平面直角坐标系中，四边形ABCD是梯形，其中A（6，0），B（3，