Question

【题目】

如图，以为直径的⊙O交△CFB的边于点A， 平分∠ABC交AC于点M，AD⊥BC于点D，AD交BM于点N，ME⊥BC于点E，AB2=AF·AC。

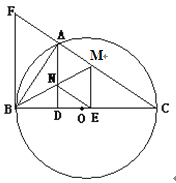
（1）证明：△ABM≌△EBM；

（2）证明：FB是⊙O的切线；

（3）若cos∠ABD=，AD=12．求四边形AMEN的面积S。

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）四边形AMEN的面积S为45.

【解析】（1）证明：∵BC是⊙O的直径，∴∠BAC=90°．

又∵EM⊥BC，BM平分∠ABC，∴AM=ME，∠AMN=∠EMN．

又∵MN=MN，∴△ANM≌△ENM．

（2）证明：∵AB2=AFAC，∴．

又∵∠BAC=∠FAB=90°，∴△ABF∽△ACB，∴∠ABF=∠C．

又∵∠FBC=∠ABC+∠FBA=90°，∴FB是⊙O的切线．

（3）解：由（1）得AN=EN，AM=EM，∠AMN=∠EMN，又∵AN∥ME，∴∠ANM=∠EMN，∴∠AMN=∠ANM，∴AN=AM，∴AM=ME=EN=AN，∴四边形AMEN是菱形．

∵cos∠ABD=，∠ADB=90°，∴．

设BD=3x，则AB=5x，由勾股定理AD==4x；

∵AD=12，∴x=3，∴BD=9，AB=15．

∵MB平分∠AME，∴BE=AB=15，∴DE=BE﹣BD=6．

∵ND∥ME，∴∠BND=∠BME．

又∵∠NBD=∠MBE，∴△BND∽△BME，∴．

设ME=x，则ND=12﹣x，，解得x=，∴S=MEDE=×6=45．