题目内容
如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径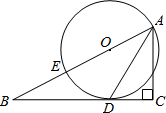 的⊙O上.
的⊙O上.
(1)求证:BC是⊙O的切线;
(2)已知∠B=28°,⊙O的半径为6,求线段AD的长.(结果精确到0.1)
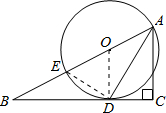 (1)证明:连接OD,
(1)证明:连接OD,∵AD平分∠BAC,∴∠BAD=∠DAC,
∵OA=OD,∴∠BAD=∠ODA,
∴∠ODA=∠DAC,
∴AC∥OD,
∵∠C=90°,∴∠ODC=90°,
即BC是⊙O的切线;
(2)解:连接DE.
∵∠B=28°,∴∠BAC=62°,
即∠BAD=31°,
∵AE为⊙O的直径,∴∠ADE=90°,
∵OA=6,∴AE=12,
∴cos∠DAE=
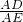 ,
,∴AD=AE•cos31°=12×0.86≈10.3.
分析:(1)连接OD,可证得AC∥OD,即可得出∠ODC=90°,即BC是⊙O的切线;
(2)连接DE,在直角三角形ADE中,利用∠BAD的余弦值求出线段AD的长.
点评:本题考查了切线的判定和性质以及解直角三角形,是基础知识要熟练掌握.

练习册系列答案
相关题目
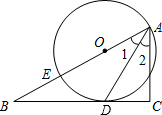 如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D,∠B=30°.求证:
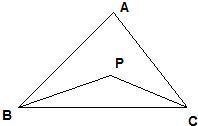
如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D,∠B=30°.求证: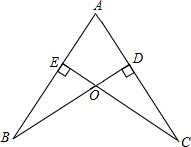 如图,已知点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D、E,求证:OB=OC.
如图,已知点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D、E,求证:OB=OC.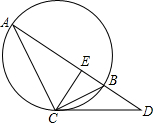 如图,已知点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A,过点C作CE⊥AB于E,CE=8,cosD=
如图,已知点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A,过点C作CE⊥AB于E,CE=8,cosD=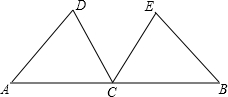 如图:已知点C在线段AB的中点,点D、E在线段AB的同侧,AD∥CE,AD=CE.
如图:已知点C在线段AB的中点,点D、E在线段AB的同侧,AD∥CE,AD=CE.