题目内容
 如图,已知点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D、E,求证:OB=OC.
如图,已知点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D、E,求证:OB=OC.分析:根据角平分线性质得出OE=OD,根据ASA证△BEO≌△CDO,根据全等三角形的性质推出即可.
解答:证明:∵点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,
∴OE=OD,∠BEO=∠CDO=90°,
在△BEO和△CDO中
∵
∴△BEO≌△CDO(ASA),
∴OB=OC.
∴OE=OD,∠BEO=∠CDO=90°,
在△BEO和△CDO中
∵
|
∴△BEO≌△CDO(ASA),
∴OB=OC.
点评:本题考查了全等三角形的性质和判定,注意:①全等三角形的对应角相等,对应边相等,②全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目

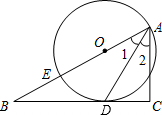 如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D,∠B=30°.求证:
如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D,∠B=30°.求证: 如图,已知点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A,过点C作CE⊥AB于E,CE=8,cosD=
如图,已知点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A,过点C作CE⊥AB于E,CE=8,cosD=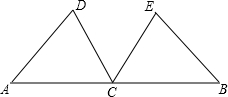 如图:已知点C在线段AB的中点,点D、E在线段AB的同侧,AD∥CE,AD=CE.
如图:已知点C在线段AB的中点,点D、E在线段AB的同侧,AD∥CE,AD=CE.