Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņń≥ ÷ĽķĶͬŰ≥Ųľ◊–ÕļŇ ÷Ľķ10Ő®ļÕ““–ÕļŇ ÷Ľķ12Ő®ļůĶńŌķ Ř∂Óő™![]() ÕÚ‘™£Ľ¬Ű≥Ųľ◊–ÕļŇ ÷Ľķ6Ő®ļÕ““–ÕļŇ ÷Ľķ9Ő®ļůĶńŌķ Ř∂Óő™
ÕÚ‘™£Ľ¬Ű≥Ųľ◊–ÕļŇ ÷Ľķ6Ő®ļÕ““–ÕļŇ ÷Ľķ9Ő®ļůĶńŌķ Ř∂Óő™![]() ÕÚ‘™£ģ
ÕÚ‘™£ģ
£®1£©«Žő ľ◊–ÕļŇ ÷ĽķļÕ““–ÕļŇ ÷Ľķ√ŅŐ® ŘľŘő™∂ŗ…Ŕ‘™£Ņ
£®2£©»Űľ◊–ÕļŇ ÷Ľķ√ŅŐ®ĹÝľŘő™1000‘™£¨““–ÕļŇ ÷Ľķ√ŅŐ®ĹÝľŘő™800‘™£¨‘§ľ∆”√≤Ľ∂ŗ”ŕ![]() ÕÚ‘™«“≤Ľ…Ŕ”ŕ
ÕÚ‘™«“≤Ľ…Ŕ”ŕ![]() ÕÚ‘™Ķń◊ ĹūĻļĹÝ’‚ŃĹ÷÷ ÷ĽķĻ≤20Ő®£¨«Žő ”–ľł÷÷ĹÝĽű∑Ĺįł?»Űňý”–ĻļĹÝĶń ÷Ľķ∂ľŅ…“‘ Ř≥Ų£¨«Ž«ů≥Ųňý”–∑Ĺįł÷–Ķń◊ÓīůņŻ»ů£ģ
ÕÚ‘™Ķń◊ ĹūĻļĹÝ’‚ŃĹ÷÷ ÷ĽķĻ≤20Ő®£¨«Žő ”–ľł÷÷ĹÝĽű∑Ĺįł?»Űňý”–ĻļĹÝĶń ÷Ľķ∂ľŅ…“‘ Ř≥Ų£¨«Ž«ů≥Ųňý”–∑Ĺįł÷–Ķń◊ÓīůņŻ»ů£ģ
°ĺīūįł°Ņ£®1£©ľ◊–ÕļŇ ÷Ľķ√ŅŐ® ŘľŘő™1500‘™, ““–ÕļŇ ÷Ľķ√ŅŐ® ŘľŘő™1400‘™£Ľ£®2£©“ĽĻ≤”–őŚ÷÷ĹÝĽű∑Ĺįł£¨ňý”–∑Ĺįł÷–◊ÓīůņŻ»ůő™11200‘™£ģ
°ĺĹ‚őŲ°Ņ
£®1£©…Ťľ◊–ÕļŇ ÷Ľķ√ŅŐ® ŘľŘő™x‘™, ““–ÕļŇ ÷Ľķ√ŅŐ® ŘľŘő™y‘™£¨łýĺ›Ő‚“‚Ĺ®ŃĘ∂Ģ‘™“Ľīő∑Ĺ≥Ő◊ť«ůĹ‚ľīŅ…£Ľ
£®2£©…Ťľ◊–ÕļŇ ÷ĽķĻļĹÝaŐ®£¨‘Ú““–ÕļŇ ÷ĽķĻļĹÝ£®20-a£©Ő®£¨łý囑§ľ∆”√≤Ľ∂ŗ”ŕ![]() ÕÚ‘™«“≤Ľ…Ŕ”ŕ
ÕÚ‘™«“≤Ľ…Ŕ”ŕ![]() ÕÚ‘™Ķń◊ ĹūĻļĹÝ’‚ŃĹ÷÷ ÷ĽķĹ®ŃĘ≤ĽĶ» Ĺ◊ť«ů≥Ų’Ż żĹ‚ľīŅ…£¨…ŤņŻ»ůő™W£¨łýĺ›Ő‚“‚Ķ√≥ŲŌŗ”¶ĶńļĮ żĻōŌĶ£¨Ň–∂Ō≥Ų‘Ųľű–‘£¨ī”∂Ý«ůň„◊ÓīůņŻ»ů£ģ
ÕÚ‘™Ķń◊ ĹūĻļĹÝ’‚ŃĹ÷÷ ÷ĽķĹ®ŃĘ≤ĽĶ» Ĺ◊ť«ů≥Ų’Ż żĹ‚ľīŅ…£¨…ŤņŻ»ůő™W£¨łýĺ›Ő‚“‚Ķ√≥ŲŌŗ”¶ĶńļĮ żĻōŌĶ£¨Ň–∂Ō≥Ų‘Ųľű–‘£¨ī”∂Ý«ůň„◊ÓīůņŻ»ů£ģ
Ĺ‚£ļ£®1£©…Ťľ◊–ÕļŇ ÷Ľķ√ŅŐ® ŘľŘő™x‘™, ““–ÕļŇ ÷Ľķ√ŅŐ® ŘľŘő™y‘™£¨łýĺ›Ő‚“‚Ķ√£ļ
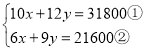
”…ĘŕĶ√£ļ![]() ĘŘ
ĘŘ
ĹęĘŘīķ»ŽĘŔĶ√£ļ![]() £¨Ĺ‚Ķ√£ļ
£¨Ĺ‚Ķ√£ļ![]()
Ĺę![]() īķ»ŽĘŘĶ√£ļ
īķ»ŽĘŘĶ√£ļ![]()
°ŗ![]()
īū£ļľ◊–ÕļŇ ÷Ľķ√ŅŐ® ŘľŘő™1500‘™, ““–ÕļŇ ÷Ľķ√ŅŐ® ŘľŘő™1400‘™£Ľ
£®2£©…Ťľ◊–ÕļŇ ÷ĽķĻļĹÝaŐ®£¨‘Ú““–ÕļŇ ÷ĽķĻļĹÝ£®20-a£©Ő®£¨łýĺ›Ő‚“‚Ķ√£ļ
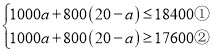
”…ĘŔĶ√£ļ![]()
”…ĘŕĶ√£ļ![]()
°ŗ≤ĽĶ» Ĺ◊ťĶńĹ‚ľĮő™£ļ![]()
’Ż żĹ‚ő™£ļ8°Ę9°Ę10°Ę11°Ę12
°ŗ»Űľ◊–ÕļŇ ÷ĽķĻļĹÝ8Ő®£¨‘Ú““–ÕļŇ ÷ĽķĻļĹÝ12Ő®£Ľ
»Űľ◊–ÕļŇ ÷ĽķĻļĹÝ9Ő®£¨‘Ú““–ÕļŇ ÷ĽķĻļĹÝ11Ő®£Ľ
»Űľ◊–ÕļŇ ÷ĽķĻļĹÝ10Ő®£¨‘Ú““–ÕļŇ ÷ĽķĻļĹÝ10Ő®£Ľ
»Űľ◊–ÕļŇ ÷ĽķĻļĹÝ11Ő®£¨‘Ú““–ÕļŇ ÷ĽķĻļĹÝ9Ő®£Ľ
»Űľ◊–ÕļŇ ÷ĽķĻļĹÝ12Ő®£¨‘Ú““–ÕļŇ ÷ĽķĻļĹÝ8Ő®£Ľ
“ĽĻ≤”–őŚ÷÷ĹÝĽű∑Ĺįł£Ľ
…ŤņŻ»ůő™W£¨łýĺ›Ő‚“‚÷™£ļ
![]()
°Ŗ![]()
°ŗWňśaĶń‘Ųīů∂Ýľű–°
°ŗĶĪ![]() Ī£¨W◊Óīů£¨◊ÓīůņŻ»ůő™£ļ
Ī£¨W◊Óīů£¨◊ÓīůņŻ»ůő™£ļ![]() ‘™
‘™
īū£ļ“ĽĻ≤”–őŚ÷÷ĹÝĽű∑Ĺįł£¨ňý”–∑Ĺįł÷–◊ÓīůņŻ»ůő™11200‘™£ģ