题目内容
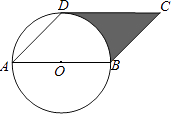
【题目】如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AB边落在AC上,点B落在点H处,折痕AE分别交BC于点E,交BO于点F,连结FH,则下列结论正确的有几个( )
⑴AD=DF;(2) ![]() =
= ![]() ;(3)
;(3) ![]() =
= ![]() ﹣1;(4)四边形BEHF为菱形.
﹣1;(4)四边形BEHF为菱形.
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解:(1)∵在正方形纸片ABCD中,折叠正方形纸片ABCD,使AB落在AC上,点B恰好与AC上的点H重合,
∴∠BAE=∠EAH=22.5°,
∴∠DAF=67.5°,
∴∠AFD=67.5°,
∴AD=DF,
故(1)正确;
⑵∵在正方形纸片ABCD中,折叠正方形纸片ABCD,使AB落在AC上,点B恰好与AC上的点H重合,
∴△ABE≌△AEH,
∴BE=EH,
∴ ![]() =
=  ,
,
故(2)正确;
⑶∵在正方形纸片ABCD中,折叠正方形纸片ABCD,使AB落在AC上,点B恰好与AC上的点H重合,
∴∠BAE=22.5°,
∴tan∠BAE=tan22.5°= ![]() ,
,
∴tan∠BAE= ![]() ,
,
故(3)正确.
⑷∵在正方形纸片ABCD中,折叠正方形纸片ABCD,使AB落在AC上,点B恰好与AC上的点H重合,
∴BE=EH,BF=FH,
又∵FH∥BC,
∴∠AEB=∠EFH,
又∵∠AEB=∠AFH,
∴∠AFH=∠EFH,
∴BE=EH=FB=BH,
∴四边形BEHF是菱形,
故(4)正确;
所以答案是:D.
【考点精析】根据题目的已知条件,利用三角形的内角和外角和角平分线的性质定理的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案【题目】声音在空气中传播的速度![]() (简称音速)与气温
(简称音速)与气温![]() 的关系如下表:
的关系如下表:
气温 | 0 | 5 | 10 | 15 | 20 |
音速 | 331 | 334 | 337 | 340 | 343 |
(1)这一变化过程中,自变量和因变量各是什么?
(2)音速![]() 与气温
与气温![]() 之间的关系式.
之间的关系式.
(3)气温![]()
![]() 时,某人看到烟花燃放
时,某人看到烟花燃放![]() 后才听到声音,那么此人与燃放烟花的所在地约相距多远?
后才听到声音,那么此人与燃放烟花的所在地约相距多远?