题目内容
已知y1=ax2+bx+c,y2=ax+b.(其中a>0),若当-1≤x≤1时,总有|y1|≤1.
(1)证明:当-1≤x≤1时,|c|≤1;
(2)若当-1≤x≤1时,y2的最大值为2.求y1的表达式.
解:(1)由-1≤x≤1时,总有|y1|≤1.
令x=0,得|c|≤1;(12分)
(2)在y1=ax2+bx+c中.令x=1得-1≤a+b+c≤1①
∵y2=ax+b.(其中a>0)的最大值为2
∴a+b=2代入①得-1≤2+c≤1-3≤c≤-1
而由(1)知-1≤c≤1
∴c=-1 (8分)
?y1=ax2+bx-1?x=0时,y1取得最小值为-1
∴故必有b=0.?a=2?y1=2x2-1.(12分)
分析:(1)取-1≤x≤1内的特殊值x=0,即可得到结论|c|≤1;
(2)根据二次函数y2的最大值为2求得a+b=2,由定义域的取值范围“-1≤x≤1”知当x=1时,-1≤a+b+c≤1①,所以联合(1)中的c的取值范围求得c=-1;然后由二次函数y1的最小值求得b=0,从而知a=2,将a、b、c的值代入二次函数y1=ax2+bx+c,即可求得y1的表达式.
点评:本题主要考查了二次函数的综合题.解答该题时,在定义域内取特殊值来求二次函数的系数,即利用待定系数法求得二次函数的解析式.
令x=0,得|c|≤1;(12分)
(2)在y1=ax2+bx+c中.令x=1得-1≤a+b+c≤1①
∵y2=ax+b.(其中a>0)的最大值为2
∴a+b=2代入①得-1≤2+c≤1-3≤c≤-1
而由(1)知-1≤c≤1
∴c=-1 (8分)
?y1=ax2+bx-1?x=0时,y1取得最小值为-1
∴故必有b=0.?a=2?y1=2x2-1.(12分)
分析:(1)取-1≤x≤1内的特殊值x=0,即可得到结论|c|≤1;
(2)根据二次函数y2的最大值为2求得a+b=2,由定义域的取值范围“-1≤x≤1”知当x=1时,-1≤a+b+c≤1①,所以联合(1)中的c的取值范围求得c=-1;然后由二次函数y1的最小值求得b=0,从而知a=2,将a、b、c的值代入二次函数y1=ax2+bx+c,即可求得y1的表达式.
点评:本题主要考查了二次函数的综合题.解答该题时,在定义域内取特殊值来求二次函数的系数,即利用待定系数法求得二次函数的解析式.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知y1=ax2+bx+c,y2=ax+b.(其中a>0),若当-1≤x≤1时,总有|y1|≤1.
(1)证明:当-1≤x≤1时,|c|≤1;
(2)若当-1≤x≤1时,y2的最大值为2.求y1的表达式.
(1)证明:当-1≤x≤1时,|c|≤1;
(2)若当-1≤x≤1时,y2的最大值为2.求y1的表达式.
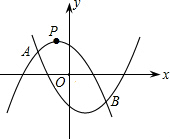

 ,且与抛物线y2=ax2-ax-1相交于A,B两点.设A,B两点的横坐标分别记为xA,xB,若在x轴上有一动点Q(x,0),且xA≤x≤xB,过q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
,且与抛物线y2=ax2-ax-1相交于A,B两点.设A,B两点的横坐标分别记为xA,xB,若在x轴上有一动点Q(x,0),且xA≤x≤xB,过q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?