题目内容
【题目】已知:在平面直角坐标系中,O为坐标原点,A(-5,8),B(3,0).
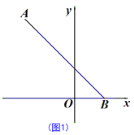
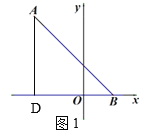
(1)如图1,求∠ABO的度数;
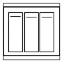
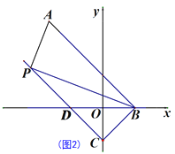
(2)如图2,点C在y轴的负半轴上,△BOC的面积为![]() ,过点C作CD∥AB交x轴于点D,点P为直线CD上一点,求△PAB的面积;
,过点C作CD∥AB交x轴于点D,点P为直线CD上一点,求△PAB的面积;
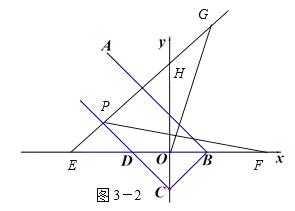
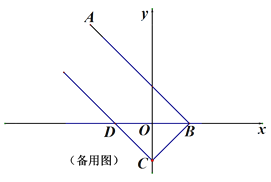
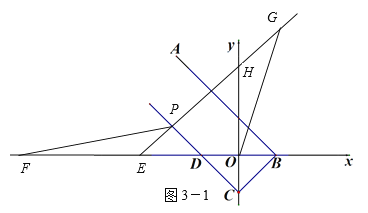
(3)如图3,在(2)的条件下,当P在第二象限时,过点P作AB的垂线交x轴于点E,点F为x轴上一点,连接PF,点G为EP延长线上一点,连接OG,若OG=FP,∠EFP+∠PGO=45°,EF=11,求点P的坐标.

【答案】(1)45°;(2)24;(3)P(-5,2)或(-7,4)
【解析】
(1)过点A作AD⊥x轴交于点D,求出AD、BD的长度即能得到答案;
(2)根据平行线间的距离处处相等,即能知道△PAB以AB为底时,高就是BC的长度,求出线段的长度,代入面积公式就能求出;
(3)分为点F在点E左侧和右侧进行讨论,根据题(2)求出PC的解析式,以及由∠EFP+∠PGO=45°推出△PFE≌△GOH,就能知道EF、OH与EO之间的关系,由EF=11,求出ED的长度后就能求出点P的横坐标,代入PC的解析式,就能求出点P的坐标.
解:(1)如图1,过点A作AD⊥x轴交于点D,
∵A(-5,8),B(3,0),
∴AD=8,BD=8,
∴△ADB是等腰直角三角形,
∴∠ABO=45°.
(2)由(1)可知,根据勾股定理可得:AB=![]() ,
,
∵△BOC的面积为![]() ,OB=3,
,OB=3,
∴ ![]() ,
,
![]() ,
,
∵点C在y轴的负半轴上,
∴C点坐标为(0,-3),
∴△BOC是等腰直角三角形,
∴∠OBC=45°,BC=![]() ,
,
∴∠ABC=∠OBC+∠ABO= 90°,
∴BC⊥AB.
∵CD∥AB,
∴点P到直线AB的距离就是BC的长度,
∴![]()
![]()
![]()
∴△PAB的面积为24.
(3)∵点G为EP延长线上一点,∠EFP+∠PGO=45°,当点G在第二象限时,∠PGO>45°,∴点G在第一象限.
当点F在点E的左边时,如图3—1所示:
由(2)可知直线PC的解析式为y=﹣x﹣3,且∠PDE= 45°,OD=3,
∵PE⊥PC,
∴∠PED= 45°,∠EHO= 45°,
∴ PE=PD,∠PEF= 135°,∠GHO= 135°.
∵∠EFP+∠PGO=45°,∠GOH+∠PGO=45°,
∴∠EFP=∠GOH.
在△PFE和△GOH中,
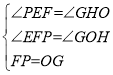 ,
,
∴△PFE≌△GOH(AAS),
∴EF=HO=11.
∴EO=HO=11,
∴DE=8,
∴点P的横坐标距离原点的距离为7,即点P的横坐标为﹣7,
将﹣7代入直线PC的解析式为y=﹣x﹣3,
则点P的纵坐标为4,
∴点P的坐标为(-7,4).
当点F在点E的左边时,如图3-2所示:
同理可证得FD=HO=EO,
∵ EF=11,
∴ EO+OF=11,
∴ EO+FD-OD=11,
∴ 2ED=11+3,
∴ ED=7,
即点P的横坐标为﹣5,
将﹣5代入直线PC的解析式为y=﹣x﹣3,
则点P的纵坐标为2,
∴点P的坐标为(-5,2).
所以点P坐标为(-5,2)或(-7,4).