题目内容
(2010•鲤城区质检)已知直线y=x+4与y轴交于点C,与x轴交于点A.(1)求线段AC的长度;
(2)若抛物线
 过点C、A,且与x轴交于另一点B,将直线AC沿y轴向下平移m个单位长度,若平移后的直线与x轴交于点D,与抛物线交于点N(N在抛物线对称轴的左边),与直线BC交于点E.
过点C、A,且与x轴交于另一点B,将直线AC沿y轴向下平移m个单位长度,若平移后的直线与x轴交于点D,与抛物线交于点N(N在抛物线对称轴的左边),与直线BC交于点E.①是否存在这样的m,使得△CAD是以AC为底的等腰三角形?若存在,请求出点N的坐标;若不存在,请说明理由;
②在直线AC平移的过程中,是否存在m值,使得△CDE的面积最大.若存在,请求出m值,若不存在,请说明理由.

【答案】分析:(1)根据直线AC的解析式,可得到A、C的坐标,进而利用勾股定理求得线段AC的长.
(2)①根据A、C的坐标,可利用待定系数法确定该抛物线的解析式,然后用m表示出平移后的直线解析式,由(1)知△OAC是等腰直角三角形,若△CAD是以AC为底的等腰三角形,那么点D必为线段CA的垂直平分线与x轴的交点,即D、O重合,由此求得m的值,进而可确定平移后的直线解析式,联立抛物线的解析式,即可求得N点的坐标.
②此题应分两种情况考虑:
1)当D在B点左侧时,即0<m≤6时;过E作EF⊥x轴于F,根据抛物线和平移后的直线解析式,可得到B、D的坐标,进而可求得BD、BA的长,由于平移前后的直线互相平行,则可证得△BDE∽△BAC,因此BD:BA=EF:OC,由此可求得EF的表达式,进而可求出△BDC和△BDE的面积,那么两个三角形的面积差即为△CDE的面积,由此可得关于S、m的函数关系式,根据函数的性质即可判断出S是否具有最大值以及对应的m的值;
2)当D在B点右侧时,即m>6时,方法同上.
解答: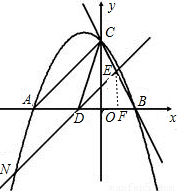 解:(1)当x=0时,y=4,
解:(1)当x=0时,y=4,
∴C(0,4)(1分)
当y=0时,x=-4,
∴A(-4,0)(2分)
在Rt△AOC中,OA=OC=4,∠AOC=90°,
∴AC=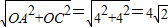 .(3分)
.(3分)
(2)①抛物线经过点A、C,则:
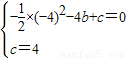 ,
,
解得 ;
;
∴抛物线所对应的函数关系式为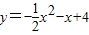 ;(4分)
;(4分)
∵△CAD是以AC为底的等腰三角形,
∴点D在AC的垂直平分线上,
此时点D与原点重合,即D(0,0),(5分)
∴m=OC=4;
则平移后的直线所对应的函数关系式为y=x,(6分)
∵点N是抛物线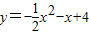 与直线y=x的交点,
与直线y=x的交点,
∴设点N(a,a),
则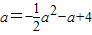 ,
,
解得a=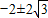 ;
;
∵点N在抛物线对称轴的左侧,
∴N(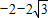 ,
, );(7分)
);(7分)
②设△CDE的面积为S,
在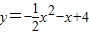 中,令y=0,
中,令y=0,
解得x=-4或x=2,
∴B(2,0),AB=6,
当点D在点B的左侧时,即当0<m≤6时(如图),
平移后的直线为y=x+4-m,
当y=0时,x=m-4.
∴D(m-4,0),
∴BD=2-(m-4)=6-m;(8分)
过点E作EF⊥AB于点F,
由DE∥AC,得∠BDE=∠CAD,
∴△BDE∽△BAC,
∴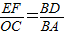 ,∴
,∴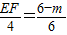 ,
,
解得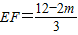 ;(9分)
;(9分)
∴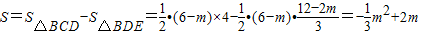 =
=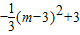 ;
;
∴抛物线的开口向下,对称轴为直线m=3,
∵顶点(3,3)的横坐标在范围0<m≤6内,
∴当m=3,S有最大值为3;(10分)
当点D在点B的右侧时,即当m>6时(如图),
平移后的直线所对应的函数关系式为y=x+4-m,
当y=0时,x=m-4,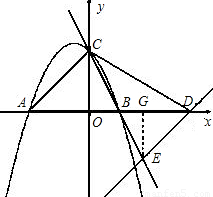
∴D(m-4,0),
∴BD=m-4-2=m-6;
过点E作EG⊥AB于点G,
由DE∥AC,得∠BDE=∠CAD,
∴△BDE∽△BAC,
∴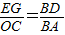 ,∴
,∴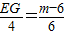 ,
,
解得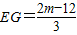 ;(11分)
;(11分)
∴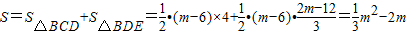 =
=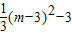 ;
;
∴抛物线开口向上,对称轴为m=3,
∵在抛物线对称轴的右侧,S随着m的增大而增大,
∴当m>6时,S没有最大值;(12分)
综上得,在直线AC平移的过程中,存在m值,当m=3,S有最大值为3,使得△CDE的面积最大.(13分)
点评:此题考查的知识点有:勾股定理、二次函数解析的确定、相似三角形的判定和性质以及图形面积的求法等重要知识;在求图形面积的最大(小)问题时,将其转化为二次函数的最值问题是常用的方法.
(2)①根据A、C的坐标,可利用待定系数法确定该抛物线的解析式,然后用m表示出平移后的直线解析式,由(1)知△OAC是等腰直角三角形,若△CAD是以AC为底的等腰三角形,那么点D必为线段CA的垂直平分线与x轴的交点,即D、O重合,由此求得m的值,进而可确定平移后的直线解析式,联立抛物线的解析式,即可求得N点的坐标.
②此题应分两种情况考虑:
1)当D在B点左侧时,即0<m≤6时;过E作EF⊥x轴于F,根据抛物线和平移后的直线解析式,可得到B、D的坐标,进而可求得BD、BA的长,由于平移前后的直线互相平行,则可证得△BDE∽△BAC,因此BD:BA=EF:OC,由此可求得EF的表达式,进而可求出△BDC和△BDE的面积,那么两个三角形的面积差即为△CDE的面积,由此可得关于S、m的函数关系式,根据函数的性质即可判断出S是否具有最大值以及对应的m的值;
2)当D在B点右侧时,即m>6时,方法同上.
解答:
 解:(1)当x=0时,y=4,
解:(1)当x=0时,y=4,∴C(0,4)(1分)
当y=0时,x=-4,
∴A(-4,0)(2分)
在Rt△AOC中,OA=OC=4,∠AOC=90°,
∴AC=
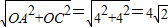 .(3分)
.(3分)(2)①抛物线经过点A、C,则:
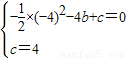 ,
,解得
 ;
;∴抛物线所对应的函数关系式为
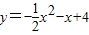 ;(4分)
;(4分)∵△CAD是以AC为底的等腰三角形,
∴点D在AC的垂直平分线上,
此时点D与原点重合,即D(0,0),(5分)
∴m=OC=4;
则平移后的直线所对应的函数关系式为y=x,(6分)
∵点N是抛物线
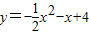 与直线y=x的交点,
与直线y=x的交点,∴设点N(a,a),
则
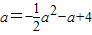 ,
,解得a=
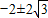 ;
;∵点N在抛物线对称轴的左侧,
∴N(
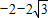 ,
, );(7分)
);(7分)②设△CDE的面积为S,
在
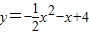 中,令y=0,
中,令y=0,解得x=-4或x=2,
∴B(2,0),AB=6,
当点D在点B的左侧时,即当0<m≤6时(如图),
平移后的直线为y=x+4-m,
当y=0时,x=m-4.
∴D(m-4,0),
∴BD=2-(m-4)=6-m;(8分)
过点E作EF⊥AB于点F,
由DE∥AC,得∠BDE=∠CAD,
∴△BDE∽△BAC,
∴
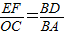 ,∴
,∴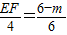 ,
,解得
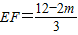 ;(9分)
;(9分)∴
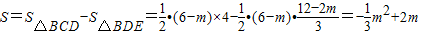 =
=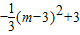 ;
;∴抛物线的开口向下,对称轴为直线m=3,
∵顶点(3,3)的横坐标在范围0<m≤6内,
∴当m=3,S有最大值为3;(10分)
当点D在点B的右侧时,即当m>6时(如图),
平移后的直线所对应的函数关系式为y=x+4-m,
当y=0时,x=m-4,

∴D(m-4,0),
∴BD=m-4-2=m-6;
过点E作EG⊥AB于点G,
由DE∥AC,得∠BDE=∠CAD,
∴△BDE∽△BAC,
∴
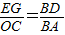 ,∴
,∴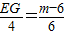 ,
,解得
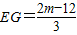 ;(11分)
;(11分)∴
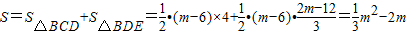 =
=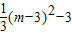 ;
;∴抛物线开口向上,对称轴为m=3,
∵在抛物线对称轴的右侧,S随着m的增大而增大,
∴当m>6时,S没有最大值;(12分)
综上得,在直线AC平移的过程中,存在m值,当m=3,S有最大值为3,使得△CDE的面积最大.(13分)
点评:此题考查的知识点有:勾股定理、二次函数解析的确定、相似三角形的判定和性质以及图形面积的求法等重要知识;在求图形面积的最大(小)问题时,将其转化为二次函数的最值问题是常用的方法.

练习册系列答案
相关题目

 的图象相交于点(a,b),则a2+b2的值是( )
的图象相交于点(a,b),则a2+b2的值是( ) 是同类二次根式的概率;
是同类二次根式的概率;
