Question

【题目】已知：如图，四边形ABCD内接于⊙O，AB＝AC，过点A作AE∥BD交CD的延长线于点E．

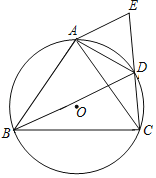
（1）求证：AE＝DE；

（2）若∠BCD﹣∠CBD＝60°，求∠ABD的度数；

（3）在（2）的条件下，若BD＝21，CD＝9，求AE的长．

Answer 1

【答案】（1）见解析；（2）30°；（3）AE的长为

【解析】

（1）根据题意得∠1＝∠ABC，∠2＝∠3，证明得到∠1＝∠2，即可证明AE＝DE；

（2）根据题意得∠5＝∠6，∠ABC＝∠4，则∠BCD＝∠4+∠6＝∠5+∠CBD+∠6，再由∠BCD﹣∠CBD＝60°，即可求出∠ABD的度数；

（3）作AM⊥BD于M，AN⊥EC于N，先证明△ADM≌△AND，求出BM和AM的值，设AE＝x，则DE＝x，NE＝x﹣6，在Rt△ANE中，根据勾股定理建立方程解出即可.

（1）证明：如图1中，

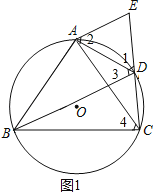
∵四边形ABCD内接于⊙O，

∴∠1＝∠ABC，

∵AE∥BD，

∴∠2＝∠3，

∵∠3＝∠4，

∵AB＝AC，

∴∠ABC＝∠4，

∴∠1＝∠2，

∴AE＝AD．

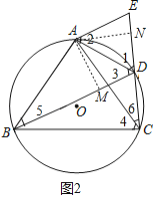
（2）解：如图2中，

∵∠5＝∠6，∠ABC＝∠4，

∴∠BCD＝∠4+∠6＝∠5+∠CBD+∠6，

∵∠BCD﹣∠CBD＝60°，

∴∠5＝∠6＝30°．

（3）解：如图2中，作AM⊥BD于M，AN⊥EC于N，

∵∠5＝∠6，AB＝AC，∠AMB＝∠ANC＝90°，

∴△AMB≌△ANC（AAS），

∴AM＝AN，BM＝CN，

∵∠3＝∠1，AD＝AD，∠AND＝∠AMD＝90°，

∴△ADM≌△ADN（AAS），

∴DN＝DM，

∴DM＝DN＝（BD﹣CD）＝6，

在Rt△AMB中，∵∠5＝30°，BM＝15，

∴BM2+AM2＝AB2，AB＝2AM，AN=AM＝5，

设AE＝x，则DE＝x，NE＝x﹣6，

在Rt△ANE中，∵AN2+NE2＝AE2，

∴（5）2+（x﹣6）2＝x2，

∴x＝，

∴AE的长为．