题目内容
已知E、F是正方形ABCD的边AB、DC的中点,点G在线段EF上,∠GDA的平分线交AE于H点,并且HG⊥GD,则∠HDA的度数为
15°
15°
.分析:根据题意作出图形,由四边形ABCD是正方形可以得出AB=BC=CD=AD,E、F是AB、DC的中点可以得出AD=2DF,利用全等三角形的性质可得GD=AD,进而得出GD=2DF,得出∠DGF=30°,有平行线的性质可得∠ADG的度数,进而求出∠HDA的度数.
解答:解:∵四边形ABCD是正方形,
∴∠A=90°,
∵HG⊥GD,
∴∠HGD=90°,
∴∠A=∠HGD=90°,
∵DH平分∠ADG,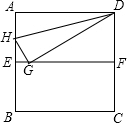
∴∠ADH=∠GDH,
又∵DH=DH,
∴△ADH≌△GHH,
∴AD=DG,
∵AB=BC=CD=AD,
∵E是AB中点,
∴DF=
DC=
AD=
DG,
∴∠DGF=30°,
∵E、F是正方形ABCD的边AB、DC的中点,
∴EF∥AD,
∴∠ADG=∠DGF=30°,
∴∠HDA=15°.
故答案为:15°.
∴∠A=90°,
∵HG⊥GD,
∴∠HGD=90°,
∴∠A=∠HGD=90°,
∵DH平分∠ADG,

∴∠ADH=∠GDH,
又∵DH=DH,
∴△ADH≌△GHH,
∴AD=DG,
∵AB=BC=CD=AD,
∵E是AB中点,
∴DF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DGF=30°,
∵E、F是正方形ABCD的边AB、DC的中点,
∴EF∥AD,
∴∠ADG=∠DGF=30°,
∴∠HDA=15°.
故答案为:15°.
点评:本题考查了正方形的性质、全等三角形的判定和全等三角形的性质以及平行线的性质和含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半,反之也成立.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
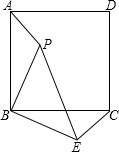 已知:点P是正方形内一点,△ABP旋转后能与△CBE重合.
已知:点P是正方形内一点,△ABP旋转后能与△CBE重合.
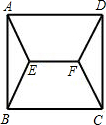 ABE=∠FDC=∠FCD=30°,∠AEF=∠DFE且AE=DF.
ABE=∠FDC=∠FCD=30°,∠AEF=∠DFE且AE=DF.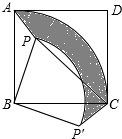 已知,点P是正方形ABCD内的一点,连接PA,PB,PC.将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图).
已知,点P是正方形ABCD内的一点,连接PA,PB,PC.将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图).