��Ŀ����
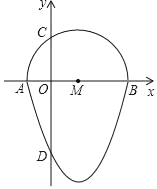
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ����A����1��0������B��3��0������C��4��y1��������D��x2��y2����������������һ�㣬�����н��ۣ��ٶ��κ���y=ax2+bx+c����СֵΪ��4a��������1��x2��4����0��y2��5a������y2��y1�� ��x2��4����һԪ���η���cx2+bx+a=0��������Ϊ��1��![]() ������ȷ���۵�����ǣ� ��
������ȷ���۵�����ǣ� ��
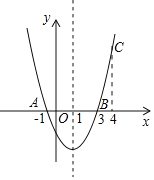
A.�٢�B.�٢�C.�ڢ�D.�٢ۢ�
���𰸡�A
��������
����A��B����д�������ߵĽ���ʽ�����![]() ������ɶ���ʽ
������ɶ���ʽ![]() �������жϢ٣���x=4ʱ��y=5a�����ݶ��κ��������ʣ������жϢڣ����ö��κ����ĶԳ��Լ������Լ����жϢۣ���
�������жϢ٣���x=4ʱ��y=5a�����ݶ��κ��������ʣ������жϢڣ����ö��κ����ĶԳ��Լ������Լ����жϢۣ���![]() ��֪b=��2a��c=��3a����cx2+bx+a=0�ɻ�Ϊ��3a x2��2a x+a=0��a��0���ⷽ�̼����жϢܣ�
��֪b=��2a��c=��3a����cx2+bx+a=0�ɻ�Ϊ��3a x2��2a x+a=0��a��0���ⷽ�̼����жϢܣ�
�⣺�����߽���ʽ���ɽ���ʽΪ![]() ��
��
��![]() ��
��
��ɶ���ʽ��![]() ��
��
�൱x=1ʱ�����κ�������СֵΪ��4a�����Ԣ���ȷ��
��x=4ʱ��![]() ��
��
�൱��1��x2��4����4a��y2��5a�����Ԣڴ���
��C�������Ϊ��4��5a����C�����ֱ��x=1�ĶԳƵ�Ϊ����2��5a����
����y2��y1���� x2��4��x2����2�����Ԣ۴���
��![]() ��֪b=��2a��c=��3a����cx2+bx+a=0�ɻ�Ϊ��3a x2��2a x+a=0��
��֪b=��2a��c=��3a����cx2+bx+a=0�ɻ�Ϊ��3a x2��2a x+a=0��
��a��0��
��̣�3a x2��2a x+a=0�����ã� 3a x2+2a x��a=0��
���![]() ��
��![]() ��
��
���Ԣ���ȷ��
���Ԣ٢���ȷ��
�ʴ�ѡ��A��