题目内容
已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP
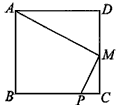
证明:∵正方形ABCD,M为CD中点
∴CM = MD =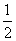 AD
AD
∵BP = 3PC ∴PC =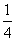 BC =
BC =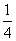 AD=
AD=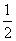 CM
CM
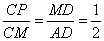
∵∠PCM =∠ADM =90°
∴△MCP∽△ADM
∴CM = MD =
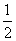 AD
AD∵BP = 3PC ∴PC =
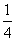 BC =
BC =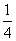 AD=
AD=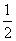 CM
CM 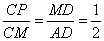
∵∠PCM =∠ADM =90°
∴△MCP∽△ADM

练习册系列答案
相关题目
 如图,已知点P是线段AB的黄金分割点,且PA>PB,若S1表示以PA为边的正方形的面积,S2表示长为AB、宽为PB的矩形的面积,那么S1( )S2.
如图,已知点P是线段AB的黄金分割点,且PA>PB,若S1表示以PA为边的正方形的面积,S2表示长为AB、宽为PB的矩形的面积,那么S1( )S2. 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直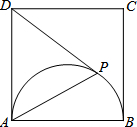 (2013•厦门质检)如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.
(2013•厦门质检)如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.