题目内容
已知O点是正方形ABCD的两条对角线的交点，则AO：AB：AC=
1：
：2
| 2 |
1：
：2
．| 2 |
分析：根据O点是正方形ABCD的两条对角线的交点得出Rt△AOB中，AB为斜边，且AO=BO，设AO=BO=1，求出AC、AB的长即可．
解答：解：∵O点是正方形ABCD的两条对角线的交点
∴Rt△AOB中，AB为斜边，且AO=BO，
设AO=BO=1，
则AC=2，
AB=
=
=
，
则AO：AB：AC=1：
：2．
故答案为：1：
：2．
∴Rt△AOB中，AB为斜边，且AO=BO，
设AO=BO=1，
则AC=2，
AB=
| AO2+BO2 |
| 12+12 |
| 2 |
则AO：AB：AC=1：
| 2 |
故答案为：1：
| 2 |
点评：本题考查了比例线段和正方形的性质，用到的知识点是正方形对角线互相垂直平分的性质、勾股定理，求AB的长是解题的关键．
练习册系列答案
相关题目
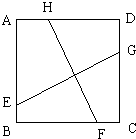如图，已知四边形ABCD是正方形，点E、F、G、H分别在AB、BC、CD、和DA上，连接EG和FH小明和小亮对这个图形进行探索，发现了很多有趣的东西，同时他俩又进一步猜想
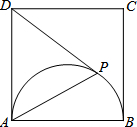（2013•厦门质检）如图，已知四边形ABCD是正方形，以AB为直径在正方形内作半圆，P是半圆上的动点（不与点A、B重合），连接PA、PD．