题目内容
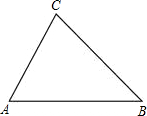 如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8.
如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8.
求:△ABC的面积.(结果可保留根号)
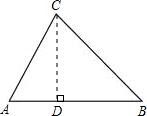 解:过C作CD⊥AB于D,
解:过C作CD⊥AB于D,在Rt△ADC中,∵∠CDA=90°,
∴
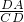 =cot∠DAC=cot60°=
=cot∠DAC=cot60°= ,
,即AD=CD×
 .
.在Rt△BDC中,∵∠B=45°,
∴∠BCD=45°,
∴CD=BD.
∵AB=DB+DA=CD+CD×
 =8,
=8,∴CD=12-4
 .
.∴S△ABC=
 AB×CD=
AB×CD= ×8×(12-4
×8×(12-4 )=48-16
)=48-16 .
.答:△ABC的面积为48-16
 .
.分析:过C作CD⊥AB于D,利用直角三角形的性质求得CD的长.已知AB的长,根据三角形的面积公式即可求得其面积.
点评:考查直角三角形的性质及三角形的面积公式的掌握情况.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
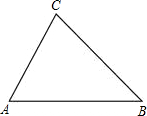 如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8.
如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8.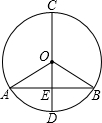 如图所示,已知:在⊙O中,BC=4
如图所示,已知:在⊙O中,BC=4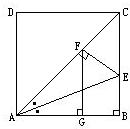 1、如图所示.已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.求证:AB2=2FG2.
1、如图所示.已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.求证:AB2=2FG2.