题目内容
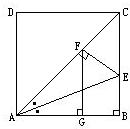 1、如图所示.已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.求证:AB2=2FG2.
1、如图所示.已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.求证:AB2=2FG2.分析:注意到正方形的特性∠CAB=45°,所以△AGF是等腰直角三角形,从而有AF2=2FG2,因而应有AF=AB,进而证明△ABE≌△AFE,即可得AF=AB,根据AF2=AG2+FG2=2FG2即可解题.
解答:证明:因为AE是∠FAB的平分线,EF⊥AF,又AE是△AFE与△ABE的公共边,
所以Rt△AFE≌Rt△ABE(AAS),
所以AF=AB.①
在Rt△AGF中,因为∠FAG=45°,
所以AG=FG,
AF2=AG2+FG2=2FG2.②
由①,②得AB2=2FG2.
所以Rt△AFE≌Rt△ABE(AAS),
所以AF=AB.①
在Rt△AGF中,因为∠FAG=45°,
所以AG=FG,
AF2=AG2+FG2=2FG2.②
由①,②得AB2=2FG2.
点评:本题考查了正方形各边长相等、各内角相等的性质,考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证Rt△AFE≌Rt△ABE是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 28、九年级甲、乙两班学生参加电脑知识竞赛,得分均为正整数,将学生成绩进行整理后分成5组,创建频率分布直方图,如图所示,已知图中从左至右的第一、第三、第四、第五小组的频率分别为0.3;0.15;0.1;0.05,且第三小组的频数为6.
28、九年级甲、乙两班学生参加电脑知识竞赛,得分均为正整数,将学生成绩进行整理后分成5组,创建频率分布直方图,如图所示,已知图中从左至右的第一、第三、第四、第五小组的频率分别为0.3;0.15;0.1;0.05,且第三小组的频数为6. 如图所示,已知A点的坐标为(6,0),B是y轴正半轴上的一动点,直线AB交直线
如图所示,已知A点的坐标为(6,0),B是y轴正半轴上的一动点,直线AB交直线 (2012•黄石)如图所示,已知A(
(2012•黄石)如图所示,已知A( 如图所示,已知边长为a的等边三角形ABC,两顶点A,分别在x轴,y轴的正半轴上滑动,连接OC,则OC长的最大值是
如图所示,已知边长为a的等边三角形ABC,两顶点A,分别在x轴,y轴的正半轴上滑动,连接OC,则OC长的最大值是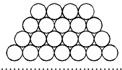 数学家高斯在读小学二年级时,老师给出了这样一道题:1+2+3+…+100=?高斯很快做出了答案,他的计算方法是:1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=50×101=5 050.根据此方法,试探究:有一堆堆放整齐的钢管其主(正)视图如图所示,已知最下面一层有钢管50根,最上面一层有4根,则共有钢管
数学家高斯在读小学二年级时,老师给出了这样一道题:1+2+3+…+100=?高斯很快做出了答案,他的计算方法是:1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=50×101=5 050.根据此方法,试探究:有一堆堆放整齐的钢管其主(正)视图如图所示,已知最下面一层有钢管50根,最上面一层有4根,则共有钢管