题目内容
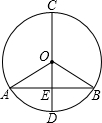 如图所示,已知:在⊙O中,BC=4
如图所示,已知:在⊙O中,BC=4| 3 |
(1)求图中扇形OAB的面积;
(2)若用扇形OAB围成一个圆锥侧面,求这个圆锥的底面圆的半径.
分析:(1)过点O作OF⊥BC于F,求得BC的长后再求得BF的长,由勾股定理求得OB的长后即可求面积;
(2)利用扇形的面积公式计算其底面半径即可.
(2)利用扇形的面积公式计算其底面半径即可.
解答:解:(1)在⊙O中,∵∠C=30°,
∴∠BOD=2∠C=60°,
∵直径CD⊥弦AB,
∴
=
,
∴∠AOB=2∠BOD=2×60°=120°,(2分)
过点O作OF⊥BC于F.
∵BC=4
,
∴BF=
BC=
×4
=2
,
设FO的长为x,则OB=2x,
在Rt△BOF中,由勾股定理得:
4x2-x2=(2
)2,
解得x=2,
∴OB=2x=4,(4分)
∴S扇形OAB=(120π×42)÷360=
π,
或S扇形OAB=(240π×42)÷360=
π;(5分)
(2)设圆锥的底面半径为r,
则4πr=
π或4πr=
π,
r=
或r=
,(9分)
答:(1)图中扇形OAB的面积为
π或
π;
(2)所求圆锥的底面半径为r=
或r=
.(10分)
∴∠BOD=2∠C=60°,
∵直径CD⊥弦AB,
∴
 |
| AD |
 |
| BD |
∴∠AOB=2∠BOD=2×60°=120°,(2分)
过点O作OF⊥BC于F.
∵BC=4
| 3 |
∴BF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
设FO的长为x,则OB=2x,
在Rt△BOF中,由勾股定理得:
4x2-x2=(2
| 3 |
解得x=2,
∴OB=2x=4,(4分)
∴S扇形OAB=(120π×42)÷360=
| 16 |
| 3 |
或S扇形OAB=(240π×42)÷360=
| 32 |
| 3 |
(2)设圆锥的底面半径为r,
则4πr=
| 16 |
| 3 |
| 32 |
| 3 |
r=
| 4 |
| 3 |
| 8 |
| 3 |
答:(1)图中扇形OAB的面积为
| 16 |
| 3 |
| 32 |
| 3 |
(2)所求圆锥的底面半径为r=
| 4 |
| 3 |
| 8 |
| 3 |
点评:本题考查了圆锥的计算,解题的关键是正确的理解圆锥的侧面展开扇形及弧长之间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
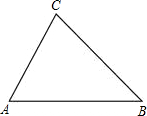 如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8.
如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8.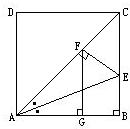 1、如图所示.已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.求证:AB2=2FG2.
1、如图所示.已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.求证:AB2=2FG2.