题目内容
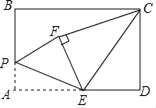
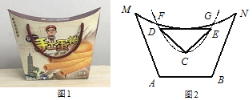
【题目】如图 1 是台湾某品牌手工蛋卷的外包装盒，其截面图如图 2 所示，盒子上方是一段圆弧（弧 MN ）.D，E 为手提带的固定点， DE 与弧MN 所在的圆相切，DE=2.手提带自然下垂时，最低点为C，且呈抛物线形，抛物线与弧MN 交于点 F，G.若△CDE 是等腰直角三角形，且点 C，F 到盒子底部 AB 的距离分别为 1，
，则弧MN 所在的圆的半径为_____．
【答案】
.
【解析】
以DE的垂直平分线为y轴，AB所在的直线为x轴建立平面直角坐标系，设抛物线的表达式为y=ax2+1，因为△CDE是等腰直角三角形，DE=2，得点E的坐标为（1，2），可得抛物线的表达式为y=x2+1，把当y
代入抛物线表达式，求得MH的长，再在Rt△FHM中，用勾股定理建立方程，求得
所在的圆的半径．
如图，以DE的垂直平分线为y轴，AB所在的直线为x轴建立平面直角坐标系，设所在的圆的圆心为P，半径为r，过F作y轴的垂线交y轴于H，设抛物线的表达式为y=ax2+1．
∵△CDE是等腰直角三角形，DE=2，∴点E的坐标为（1，2），代入抛物线的表达式，得：2=a+1，a=1，∴抛物线的表达式为y=x2+1，当y时，即
，解得：
，∴FH
．
∵∠FHM=90°，DE与所在的圆相切，∴
，解得：
，∴所在的圆的半径为．
故答案为：．
【题目】某甜品店用 A，B 两种原料制作成甲、乙两款甜品进行销售，制作每份甜品的原料所需用量如下表所示．该店制作甲款甜品 x 份，乙款甜品 y 份，共用去A 原料 2000 克．
原料 款式 | A 原料(克) | B 原料(克) |
甲款甜品 | 30 | 15 |
乙款甜品 | 10 | 20 |
（1）求 y 关于 x 的函数表达式．
（2）已知每份甲甜品的利润为 a 元(a 正整数)， 每份乙甜品的利润为 2 元. 假设两款甜品均能全部卖出．
①当 a=3 时，若获得总利润不少于 220 元，则至少要用去 B 原料多少克？
②现有 B 原料 3100 克，要使获利为 450 元且尽量不浪费原材料，甲甜品的每份利润应定为多元？
