题目内容
已知:如图,P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,BC∥OP交⊙O于点C.(1)判断直线PC与⊙O的位置关系,并证明你的结论;
(2)若BC=2,
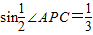 ,求PC的长及点C到PA的距离.
,求PC的长及点C到PA的距离.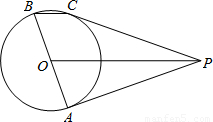
【答案】分析:(1)连接OC,由BC∥OP,∠1=∠2,∠3=∠4,而∠1=∠3,得到∠2=∠4,易证得△POC≌△POA,则∠PCO=∠PAO,由PA切⊙O于点A,根据切线的性质得到∠PAO=90°,则有∠PCO=90°,根据切线的判定得到PC与⊙O相切;
(2)连AC、过点C作CD⊥PA于D,由△POC≌△POA,则∠5=∠6= ∠APC,于是有sin∠5=sin
∠APC,于是有sin∠5=sin ∠APC=
∠APC= ,利用互余公式得到cos∠2=sin∠5=
,利用互余公式得到cos∠2=sin∠5= ,则cos∠3=
,则cos∠3= ,由于AB是⊙O的直径,得到∠ACB=90°,然后利用余弦的定义可计算出AB=6,利用勾股定理可计算出AC=4
,由于AB是⊙O的直径,得到∠ACB=90°,然后利用余弦的定义可计算出AB=6,利用勾股定理可计算出AC=4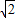 ,且OC=3,在Rt△POC中,OC=3,sin∠5=
,且OC=3,在Rt△POC中,OC=3,sin∠5= =
=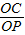 ,可计算出OP,然后根据勾股定理可计算出PC的长;在Rt△CAD中,利用cos∠8=
,可计算出OP,然后根据勾股定理可计算出PC的长;在Rt△CAD中,利用cos∠8=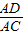 =
=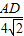 =
= 可计算得到AD,然后再根据勾股定理即可计算出CD的长.
可计算得到AD,然后再根据勾股定理即可计算出CD的长.
解答:解:(1)直线PC与⊙O相切.理由如下: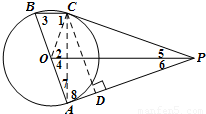
连接OC,
∵BC∥OP,
∴∠1=∠2,∠3=∠4.
∵OB=OC,
∴∠1=∠3.
∴∠2=∠4.
又∵OC=OA,OP=OP,
∴△POC≌△POA,
∴∠PCO=∠PAO.
∵PA切⊙O于点A,
∴∠PAO=90°,
∴∠PCO=90°,
∴PC与⊙O相切;
(2)连AC,如图,
∵△POC≌△POA,
∴∠5=∠6= ∠APC,
∠APC,
∴sin∠5=sin ∠APC=
∠APC= ,
,
∵∠PCO=90°,
∴∠2+∠5=90°,
∴cos∠2=sin∠5= ,
,
∵∠3=∠1=∠2,
∴cos∠3= ,
,
∵AB是⊙O的直径,
∴∠ACB=90°.
∴cos∠3=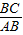 =
=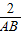 =
= ,
,
∴AB=6,
∴OA=OB=OC=3,AC=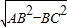 =4
=4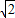 ,
,
在Rt△POC中,OC=3,sin∠5= =
=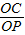 ,
,
∴OP=9,
∴PC=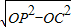 =6
=6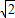 ,
,
过点C作CD⊥PA于D,
∵∠ACB=∠PAO=90°,
∴∠3+∠7=90°,∠7+∠8=90°.
∴∠3=∠8.
∴cos∠8=cos∠3= ,
,
在Rt△CAD中,cos∠8=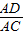 =
=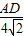 =
= ,
,
∴AD=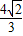 ,
,
∴CD=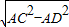 =
=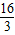 ,
,
即点C到PA的距离为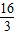 .
.
点评:本题考查了圆的综合题:过半径的外端点且垂直于半径的直线为圆的切线;圆的切线垂直于过切点的直线;直角所对的圆周角为直角;常用三角函数和勾股定理解决圆的计算问题.
(2)连AC、过点C作CD⊥PA于D,由△POC≌△POA,则∠5=∠6=
 ∠APC,于是有sin∠5=sin
∠APC,于是有sin∠5=sin ∠APC=
∠APC= ,利用互余公式得到cos∠2=sin∠5=
,利用互余公式得到cos∠2=sin∠5= ,则cos∠3=
,则cos∠3= ,由于AB是⊙O的直径,得到∠ACB=90°,然后利用余弦的定义可计算出AB=6,利用勾股定理可计算出AC=4
,由于AB是⊙O的直径,得到∠ACB=90°,然后利用余弦的定义可计算出AB=6,利用勾股定理可计算出AC=4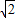 ,且OC=3,在Rt△POC中,OC=3,sin∠5=
,且OC=3,在Rt△POC中,OC=3,sin∠5= =
=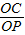 ,可计算出OP,然后根据勾股定理可计算出PC的长;在Rt△CAD中,利用cos∠8=
,可计算出OP,然后根据勾股定理可计算出PC的长;在Rt△CAD中,利用cos∠8=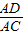 =
=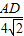 =
= 可计算得到AD,然后再根据勾股定理即可计算出CD的长.
可计算得到AD,然后再根据勾股定理即可计算出CD的长.解答:解:(1)直线PC与⊙O相切.理由如下:

连接OC,
∵BC∥OP,
∴∠1=∠2,∠3=∠4.
∵OB=OC,
∴∠1=∠3.
∴∠2=∠4.
又∵OC=OA,OP=OP,
∴△POC≌△POA,
∴∠PCO=∠PAO.
∵PA切⊙O于点A,
∴∠PAO=90°,
∴∠PCO=90°,
∴PC与⊙O相切;
(2)连AC,如图,
∵△POC≌△POA,
∴∠5=∠6=
 ∠APC,
∠APC,∴sin∠5=sin
 ∠APC=
∠APC= ,
,∵∠PCO=90°,
∴∠2+∠5=90°,
∴cos∠2=sin∠5=
 ,
,∵∠3=∠1=∠2,
∴cos∠3=
 ,
,∵AB是⊙O的直径,
∴∠ACB=90°.
∴cos∠3=
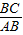 =
=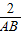 =
= ,
,∴AB=6,
∴OA=OB=OC=3,AC=
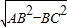 =4
=4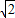 ,
,在Rt△POC中,OC=3,sin∠5=
 =
=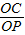 ,
,∴OP=9,
∴PC=
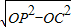 =6
=6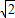 ,
,过点C作CD⊥PA于D,
∵∠ACB=∠PAO=90°,
∴∠3+∠7=90°,∠7+∠8=90°.
∴∠3=∠8.
∴cos∠8=cos∠3=
 ,
,在Rt△CAD中,cos∠8=
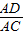 =
=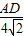 =
= ,
,∴AD=
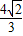 ,
,∴CD=
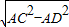 =
=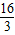 ,
,即点C到PA的距离为
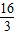 .
.点评:本题考查了圆的综合题:过半径的外端点且垂直于半径的直线为圆的切线;圆的切线垂直于过切点的直线;直角所对的圆周角为直角;常用三角函数和勾股定理解决圆的计算问题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
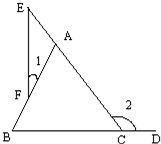 28、已知:如图,E是△ABC的边CA延长线上一点,F是AB上一点,D点在BC的延长线上.试证明∠1<∠2.
28、已知:如图,E是△ABC的边CA延长线上一点,F是AB上一点,D点在BC的延长线上.试证明∠1<∠2.
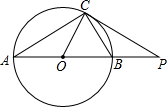 (2004•西藏)已知,如图,P是⊙O外一点,PC切⊙O于点C,割线PO交⊙O于点B、A,且AC=PC.
(2004•西藏)已知,如图,P是⊙O外一点,PC切⊙O于点C,割线PO交⊙O于点B、A,且AC=PC.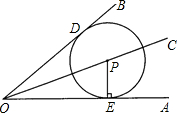 已知:如图,P是∠AOB的角平分线OC上一点.PE⊥OA于E.以P点为圆心,PE长为半径作⊙P.求证:⊙P与OB相切.
已知:如图,P是∠AOB的角平分线OC上一点.PE⊥OA于E.以P点为圆心,PE长为半径作⊙P.求证:⊙P与OB相切.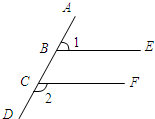 已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF.
已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF.