题目内容
【题目】如图,已知AB是⊙O的直径,C是⊙O上的一点,连结AC并延长至D,使CD=AC,连结BD,作CE⊥BD,垂足为E.
(1)线段AB与DB的大小关系为___________,请证明你的结论;
(2)求证:CE 是⊙O的切线;
(3)当△CED与四边形ACEB的面积比是1:7时,试判断△ABD的形状,并证明.

【答案】(1)AB=DB;(2)见解析;(3)△ABD为等边三角形,理由见解析
【解析】试题分析:(1)首先连接BC,由AB是⊙O的直径,可得∠ACB=90°,又由AC=CD,利用三线合一的知识,即可判定AB=DB;
(2)首先连接OC,由点O为AB的中点,点C为AD的中点,根据三角形中位线的性质,可证得OC∥BD,又由CE⊥BD,即可证得CE⊥OC,即得CE与⊙O的切线;
(3)易证得△CED∽△BCD,然后由相似三角形的对应边成比例证得:CD:BD=1:2,可求得∠CBD=30°,即可得∠D=60°,则可证得△ABD是等边三角形.
试题解析:(1)AB=DB,证明如下:
连结BC,∵AB是⊙O的直径,∴∠ACB=90°,即BC⊥AD,
又∵AC=CD,∴BC垂直平分线段AD,∴AB=DB;
(2)连接OC,
∵点O为AB的中点,点C为AD的中点,∴OC为△ABD的中位线,∴OC//BD,
又∵CE⊥BD,∴CE⊥OC,∴CE是⊙O的切线;
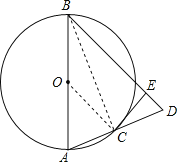
(3)△ABD是等边三角形,证明如下:
由![]() =
=![]() ,
,
得![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,∴
,∴![]() =
=![]() ,
, ![]() =
=![]() ,
,
∵∠D=∠D,∠CED=∠BCD=90°,∴△CED∽△BCD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
在Rt△BCD中,∵sin∠CBD=![]() =
=![]() ,
,
∴∠CBD=30°,∴∠D=60°,
又∵AB=DB,∴△ABD是等边三角形.

练习册系列答案
相关题目