题目内容
【题目】在由6个边长为1的小正方形组成的方格中:
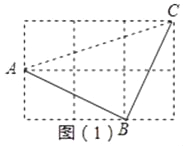
(1)如图(1),A、B、C是三个格点(即小正方形的顶点),判断AB与BC的关系,并说明理由;
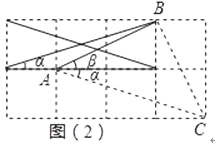
(2)如图(2),连结三格和两格的对角线,求∠α+∠β的度数(要求:画出示意图并给出证明)

【答案】(1) AB与BC是垂直且相等.(2) 45°.
【解析】试题分析:(1)如图(1),根据勾股定理,判断出AB2+BC2=AC2,即可推得△ABC是直角三角形,据此判断出AB与BC的关系,并说明理由即可.
(2)如图(2),根据勾股定理,判断出AB2+BC2=AC2,即可推得△ABC是等腰直角三角形,据此求出∠α+∠β的度数是多少即可.
试题解析:
(1)如图(1),连接AC,
 ,
,
由勾股定理得,AB2=12+22=5,
BC2=12+22=5,
AC2=12+32=10,
∴AB2+BC2=AC2,AB=BC,
∴△ABC是直角三角形,∠ABC=90°,
∴AB⊥BC
∴AB与BC是垂直且相等.
(2)∠α+∠β=45°.
证明:如图(2),
 ,
,
由勾股定理得,AB2=12+22=5,
BC2=12+22=5,
AC2=12+32=10,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,
∵AB=BC,
∴△ABC是等腰直角三角形,
∴∠α+∠β=45°.

【题目】一只不透明的袋子中装有4个小球,分别标有数字2,3,4,![]() ,这些球除数字外都相同.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和.记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表:
,这些球除数字外都相同.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和.记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表:
摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为7”出现的频数 | 1 | 9 | 14 | 24 | 26 | 37 | 58 | 82 | 109 | 150 |
“和为7”出现的频率 | 0.10 | 0.45 | 0.47 | 0.40 | 0.29 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
试估计出现“和为7”的概率为________.