题目内容
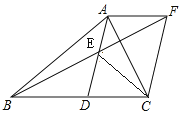
【题目】如图,直线经过矩形![]() 的对角线
的对角线![]() 的中点
的中点![]() ,分别与矩形的两边相交于点
,分别与矩形的两边相交于点![]() 、
、![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,则四边形
,则四边形![]() 是______形,并说明理由;
是______形,并说明理由;
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)菱,理由见解析;(3)![]() .
.
【解析】
(1)根据矩形的性质得到AD∥BC,根据平行线的性质得到∠EDO=∠FBO,由全等三角形的判定定理即可得到结论;
(2)根据平行四边形的判定定理得到四边形BEDF是平行四边形,由菱形的判定定理即可得到结论;
(3)根据勾股定理得到![]() ,设BE=DE=x,得到AE=8-x,根据勾股定理列方程得到
,设BE=DE=x,得到AE=8-x,根据勾股定理列方程得到![]() ,根据三角形的面积公式即可得到结论.
,根据三角形的面积公式即可得到结论.
解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EDO=∠FBO,
∵点O是BD的中点,
∴BO=DO,
在△BOF与△DOE中,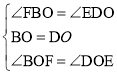 ,
,
∴△BOF≌△DOE(ASA),
∴OE=OF;
(2)四边形BEDF是菱形,
理由:∵OE=OF,OB=OD,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF是菱形;
故答案为:菱;
(3)∵四边形ABCD是矩形,
∴∠A=90°,
∵AD=8,BD=10,
![]() ,
,
设BE=DE=x,
∴AE=8﹣x,
∵AB2+AE2=BE2,
∴62+(8﹣x)2=x2,
解得:![]() ,
,
∴BE=![]() ,
,
∵BO=![]() BD=5,
BD=5,
∴OE=![]() ,
,
∴△BDE的面积![]() .
.


 名校课堂系列答案
名校课堂系列答案【题目】某学校计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为6000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠25% |
乙商场 | 每台优惠20% |
(1)设学校购买![]() 台电脑,选择甲商场时,所需费用为
台电脑,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现在因为急需,计划从甲乙两商场一共买入10台电脑,已知甲商场的运费为每台50元,乙商场的运费为每台60元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?