Question

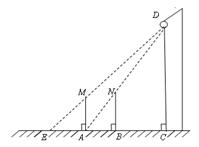
已知：如图，在△ABC中，AB="AC=" 5，BC= 8，D，E分别为BC，AB边上一点，∠ADE=∠C．

（1）求证：△BDE∽△CAD；
（2）若CD=2，求BE的长．

Answer 1

（1）证明见解析；（2）2.4.

解析试题分析：（1）由题中条件可得∠B=∠C，所以由已知条件，求证∠BDE=∠CAD即可得△BDE∽△CA；（2）由（1）可得△BDE∽△CAD，进而由相似三角形的对应边成比例，即可求解线段的长．
试题解析：（1）∵ AB=AC，∴∠B=∠C．
∵∠ADE+∠BDE=∠ADB =∠C+∠CAD，且∠ADE=∠C，∴∠BDE =∠CAD．
∴△BDE∽△CAD．
（2）由（1）△BDE∽△CAD得．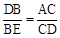
∵ AB="AC=" 5，BC= 8，CD=2，∴．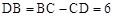
∴．
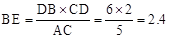考点：相似三角形的判定与性质.