题目内容
已知⊙O1和⊙O2的半径分别是8.5cm和3.5cm,当两圆外切时圆心距为d1,两圆内切时圆心距为d2,如图,以d1和d2长为邻边作矩形ABCD,依次连接矩形ABCD四边中点,得四边形EFGH,则四边形EFGH周长是______cm.
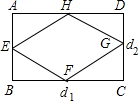

根据题意,得
d1=8.5+3.5=12cm,d2=8.5-3.5=5cm,
故AD=BC=12cm,AB=CD=5cm;
连接AC,BD,
由勾股定理,得AC=
=
=13,
同理可得BD=13,
由三角形的中位线定理,得
EH=GF=
BD=
×13=
;EF=HG=
AC=
×13=
.
则四边形EFGH周长是=4EF=4×
=26(cm).
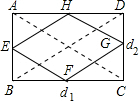
d1=8.5+3.5=12cm,d2=8.5-3.5=5cm,
故AD=BC=12cm,AB=CD=5cm;
连接AC,BD,
由勾股定理,得AC=
| AD2+CD2 |
| 122+52 |
同理可得BD=13,
由三角形的中位线定理,得
EH=GF=
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
则四边形EFGH周长是=4EF=4×
| 13 |
| 2 |


练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
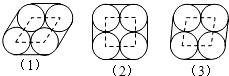 线)分别构成菱形、正方形、菱形,如果把三种方式所用绳子的长度分别用x,y,z来表示,则( )
线)分别构成菱形、正方形、菱形,如果把三种方式所用绳子的长度分别用x,y,z来表示,则( )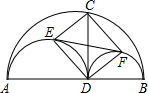 半圆,EF是这两个半圆的外公切线,E、F为切点.
半圆,EF是这两个半圆的外公切线,E、F为切点.