题目内容
【题目】(6分)如图是甲、乙两人同一地点出发后，路程随时间变化的图象．
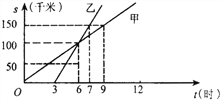
（1）此变化过程中，__________是自变量，_________是因变量．
（2）甲的速度是 ________千米/时，乙的速度是________千米/时
（3）9时甲在乙的________（前面、后面、相同位置）
（4）6时表示____________________________
【答案】 时间 路程 
后面 乙追上甲
【解析】分析：（1）根据自变量与因变量的含义得到时间是自变量，路程是因变量；
（2）甲走6行驶100千米，乙走3小时行驶了100千米，则可得到它们的速度的大小；
（3）观察图象得到t=9时，乙的图象在甲的上方，即乙行驶的路程远些；（4）6时两图象相交，说明他们相遇；
本题解析：
(1)函数图象反映路程随时间变化的图象，则时间是自变量，路程为因变量；
(2)甲的速度=
千米/小时,乙的速度=
千米/小时；
(3)t=9时，乙的图象在甲的上方，即乙行驶的路程远些，所以9时甲在乙的后面
(4)6时表示他们相遇，即乙追赶上了甲；
练习册系列答案
相关题目
【题目】今年5月，某大型商业集团随机抽取所属的m家商业连锁店进行评估，将各连锁店按照评估成绩分成了A、B、C、D四个等级，绘制了如图尚不完整的统计图表．
评估成绩n（分） | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n＜90 | B | |
70≤n＜80 | C | 15 |
n＜70 | D | 6 |
根据以上信息解答下列问题：
（1）求m的值；
（2）在扇形统计图中，求B等级所在扇形的圆心角的大小；（结果用度、分、秒表示）
（3）从评估成绩不少于80分的连锁店中任选2家介绍营销经验，求其中至少有一家是A等级的概率．
