��Ŀ����
����Ŀ������̽����
��1����֪ѧϰ
�����ε���λ�ߣ��������������е���߶ν������ε���λ�ߣ�
�����ε���λ�����ʣ����ε���λ��ƽ�������ף����ҵ������͵�һ�룮
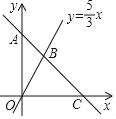
�������ʽ ![]() ��mΪ��������m��0������x��0����
��mΪ��������m��0������x��0���� ![]() �����������н��ۣ�
�����������н��ۣ�
��x ������ʱ����ĸx+2m������ʽ ![]() ��ֵ���ٲ�����0�����Դ���0����x ����ʱ����ĸx+2m���٣���ʽ
��ֵ���ٲ�����0�����Դ���0����x ����ʱ����ĸx+2m���٣���ʽ ![]() ��ֵ����������
��ֵ���������� ![]() ��������
�������� ![]() ��������
�������� ![]() ��
��
��2��������
��ͼ2����֪������ABCD�У�AD��BC��AD��BC��E��F�ֱ���AB��CD���е㣮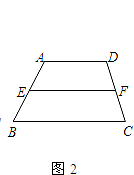
��1����AD=7��BC=17���� ![]() ��ֵ��
��ֵ��
��2����AD=a��aΪ���ij�������BC=x�����ʣ���BC�ij���������ʱ�� ![]() ��ֵ�ܷ���ڻ����3����֤����Ľ��ۣ�
��ֵ�ܷ���ڻ����3����֤����Ľ��ۣ�
��3����һ�����룺�κ�һ�����ε���λ�����ֳɵ�������ͼ�ε�����ı�ֵ���ڵķ�Χ��ʲô����˵�����ɣ�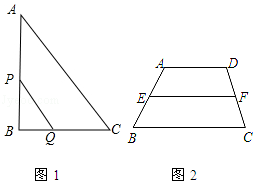
���𰸡�
��1��
�⣺������ADFE�ĸ�Ϊh��������BCFE�ĸ�Ϊh��
��E��F�ֱ���AB��CD���е㣬
��EF������ABCD����λ�ߣ�
��EF��AD��BC��EF= ![]() ��AD+BC��=
��AD+BC��= ![]() ��7+17��=12��
��7+17��=12��
�� ![]() =
= 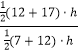 =
= ![]()
��2��
�⣺��BC�ij���������ʱ�� ![]() ��ֵ���ܴ��ڻ����3���������£�
��ֵ���ܴ��ڻ����3���������£�
��E��F�ֱ���AB��CD���е㣬
��EF������ABCD����λ�ߣ�
��EF= ![]() ��AD+BC��=
��AD+BC��= ![]() ��a+x����
��a+x����
�ɣ�1���ã� ![]() =
=  =
= ![]() ��
��
��BC�ij�x��������ʱ�� ![]() �ķ���a+3x���������ڣ�������3������С��3��
�ķ���a+3x���������ڣ�������3������С��3��
�൱BC�ij���������ʱ�� ![]() ��ֵ���ܴ��ڻ����3
��ֵ���ܴ��ڻ����3
��3��
�⣺�κ�һ�����ε���λ�����ֳɵ�������ͼ�ε�����ı�ֵ���ڵķ�Χ�Ǵ���1��С��3���������£�
�ɣ�2���ã� ![]() =
= ![]() ��3����x ����ʱ����ĸ3a+x���٣�x����a��
��3����x ����ʱ����ĸ3a+x���٣�x����a��
��a+3x����4a��3a+x����4a��
�� ![]() =
= ![]() ��ֵ����1��������1��
��ֵ����1��������1��
��1�� ![]() ��3��
��3��
���κ�һ�����ε���λ�����ֳɵ�������ͼ�ε�����ı�ֵ���ڵķ�Χ�Ǵ���1��С��3
����������������1��������ADFE�ĸ�Ϊh��������BCFE�ĸ�Ϊh��֤��EF������ABCD����λ�ߣ���������λ�߶����ó�EF��AD��BC��EF= ![]() ��AD+BC��=12�������������ʽ���ɵó��𰸣���2����������λ�߶����ó�EF=
��AD+BC��=12�������������ʽ���ɵó��𰸣���2����������λ�߶����ó�EF= ![]() ��AD+BC��=
��AD+BC��= ![]() ��a+x�����ɣ�1���ã�
��a+x�����ɣ�1���ã� ![]() =
=  =
= ![]() ����BC�ij�x��������ʱ��
����BC�ij�x��������ʱ�� ![]() �ķ���a+3x���������ڣ�������3������С��3����3���ɣ�2���ã�
�ķ���a+3x���������ڣ�������3������С��3����3���ɣ�2���ã� ![]() =
= ![]() ��3����x ����ʱ����ĸ3a+x���٣�x����a����a+3x����4a��3a+x����4a���ó�
��3����x ����ʱ����ĸ3a+x���٣�x����a����a+3x����4a��3a+x����4a���ó� ![]() =
= ![]() ��ֵ����1��������1�����ɵó��𰸣�
��ֵ����1��������1�����ɵó��𰸣�
�����㾫����������Ŀ����֪�������������ε���λ�ߵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ�������ε���λ��ƽ�������ε����ײ��������͵�һ�룮

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ���ڶ����»�У�ijУ����ȫ��ʦ���������飬Ϊ�˽������鼮�����࣬ͼ�����Ա�Բ����鼮�����˳������飬���ݵ������ݻ��������²�������ͳ��ͼ�����������ͳ��ͼ�����ṩ����Ϣ�ش��������⣺ ijУʦ�������������ͳ�Ʊ�
���� | Ƶ�� | �ٷֱ� |
A�������� | 12 | 30% |
B����ѧ�� | n | 35% |
C�������� | m | 20% |
D�������� | 6 | 15% |
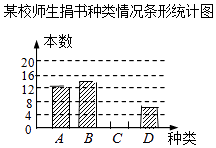
��1��ͳ�Ʊ��е�n= �� ����ȫ����ͳ��ͼ��
��2�����λʦ��������2000����������ж��ٱ�������ͼ�飿