题目内容
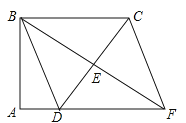
【题目】如图,在四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.
(1)求证:四边形BDFC是平行四边形;
(2)若CB=CD,求四边形BDFC的面积.
【答案】(1)见解析 (2)3![]()
【解析】
(1)证明△BEC△FED,利用一组对边平行且相等的四边形是平行四边形即可判定.
(2)过C点作CH⊥AF,可证四边形ABCH为矩形,求得DH的长,利用勾股定理求出CH的长,利用平行四边形的面积公式即可求解.
(1)∵∠A=∠ABC=90°
∴BC∥AF
∴∠BCD=∠FDE,∠CBE=∠DFE
又∵点E是边CD的中点
∴CE=DE
∴△BCE△FDE(AAS)
∴BC=DF
又BC∥DF
∴四边形BDFC是平行四边形
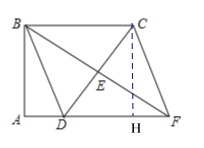
(2) )过C点作CH⊥AF于H点.
则∠AHC=∠A=∠ABC=90°
∴四边形ABCH为矩形
∴AH=BC=3
∵AD=1
∴DH=2
又∵CB=CD
∴CD=3
根据勾股定理得:CH=![]()
∴S四边形BDFC=3![]()

练习册系列答案
相关题目
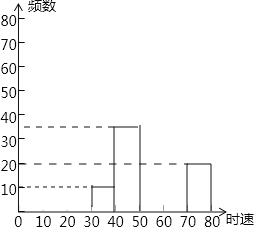
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30﹣40含起点值30,不含终点值40),得到其频数及频率如表:
数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | c |
50﹣60 | a | 0.39 |
60﹣70 | b | d |
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |
(1)表中a、b、c、d分别为:a= ; b= ; c= ; d=
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?