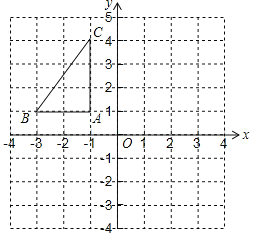��Ŀ����
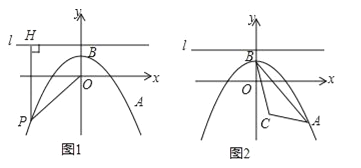
����Ŀ����ͼ1����ƽ��ֱ������ϵxOy�У�������![]() ������A��4����3��������Ϊ��B����PΪ�������ϵ�һ�����㣬l�ǹ��㣨0��2���Ҵ�ֱ��y���ֱ�ߣ���P��PH��l������ΪH������PO��
������A��4����3��������Ϊ��B����PΪ�������ϵ�һ�����㣬l�ǹ��㣨0��2���Ҵ�ֱ��y���ֱ�ߣ���P��PH��l������ΪH������PO��
��1���������ߵĽ���ʽ����д���䶥��B�����ꣻ
��2���ٵ�P���˶���A�㴦ʱ�����㣺PO= ��PH= ���ɴ˷��֣�PO PH�����������������=������
�ڵ�P�������������˶�ʱ������PO��PH��ʲô������ϵ����֤����IJ��룻
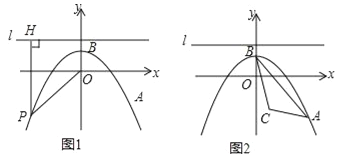
��3����ͼ2�����C��1����2�������Ƿ���ڵ�P��ʹ����P��O��HΪ��������������ABC���ƣ������ڣ����P������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ������B��0��1������2����5��5=����PO=PH����3��P��1��
������B��0��1������2����5��5=����PO=PH����3��P��1��![]() ����1��
����1��![]() ����
����
��������
�����������1�����ô���ϵ�������ɽ�����⣮
��2�������PO��PH���ɽ�����⣮
�ڽ��ۣ�PO=PH�����P���꣨m��![]() ������������֮����빫ʽ���PH��PO���ɽ�����⣮
������������֮����빫ʽ���PH��PO���ɽ�����⣮
��3�������ж�PH��BC��PO��AC�Ƕ�Ӧ�ߣ����P��m��![]() ������
������![]() �г����̼��ɽ�����⣮
�г����̼��ɽ�����⣮
�����������1���⣺��������![]() ������A��4����3�����ੁ3=16a+1����a=
������A��4����3�����ੁ3=16a+1����a=![]() ���������߽���ʽΪ
���������߽���ʽΪ![]() ������B��0��1����
������B��0��1����
��2���ٵ�P���˶���A�㴦ʱ����PO=5��PH=5����PO=PH���ʴ𰸷ֱ�Ϊ��5��5=��
�ڽ��ۣ�PO=PH�����ɣ����P���꣨m��![]() ������PH=2����
������PH=2����![]() ��=
��=![]() ��PO=
��PO=![]() ����PO=PH��
����PO=PH��
��3����BC=![]() =
=![]() ��AC=
��AC=![]() =
=![]() ��AB=
��AB=![]() =
=![]() ����BC=AC����PO=PH���֡���P��O��HΪ��������������ABC���ƣ���PH��BC��PO��AC�Ƕ�Ӧ�ߣ���
����BC=AC����PO=PH���֡���P��O��HΪ��������������ABC���ƣ���PH��BC��PO��AC�Ƕ�Ӧ�ߣ���![]() �����P��m��
�����P��m��![]() ������
������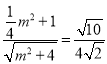 �����m=��1�����P���꣨1��
�����m=��1�����P���꣨1��![]() ����1��
����1��![]() ����
����

 ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�