Question

【题目】如图，△ABC与△ADE都是等腰直角三角形，∠C和∠AED都是直角，点E在AB上，如果，△ABC旋转后能与△ADE重合，那么哪一点是旋转中心？旋转了多少度？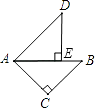

Answer 1

【答案】解：∵△ABC与△ADE是两个全等的等腰直角三角形，

∴∠BAC=∠DAE=45°，

根据图形，△ABC以点A为旋转中心逆时针旋转45°与△ADE重合．

答：点A是旋转中心；旋转了45度．

【解析】首先根据等腰直角三角形的性质可得到∠BAC=45°，然后再结合图形，依据旋转中心以及旋转角的定义可得到问题的答案.
【考点精析】掌握等腰直角三角形和旋转的性质是解答本题的根本，需要知道等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．