题目内容
 (2009•裕华区一模)已知抛物线y=x2+bx+c的部分图象;如图
(2009•裕华区一模)已知抛物线y=x2+bx+c的部分图象;如图(1)求该抛物线的表达式;
(2)写出该抛物线的顶点坐标;
(3)观察图象指出,当x分别取何值时,有y>0,y<0;
(4)若抛物线与x轴的交点分别为点A与点B(A在B左侧),在x轴上方的抛物线上是否存在点P,使S△PAB=8?若存在,请求出P点坐标;若不存在,请说明理由.
分析:(1)根据图象上的点的坐标有:(-1,0),对称轴为:x=1,代入解析式求出即可;
(2)利用配方法直接求出即可;
(3)利用图象与x轴交点坐标,得出x取值范围即可;
(4)利用S△PAB=8,AB=4,求出P点纵坐标,即可得出横坐标即可.
(2)利用配方法直接求出即可;
(3)利用图象与x轴交点坐标,得出x取值范围即可;
(4)利用S△PAB=8,AB=4,求出P点纵坐标,即可得出横坐标即可.
解答: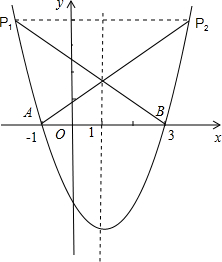 解:(1)∵抛物线y=x2+bx+c的部分图象可得:
解:(1)∵抛物线y=x2+bx+c的部分图象可得:
图象经过:(-1,0),对称轴为:x=1,
∴
,
解得:
,
∴该抛物线的表达式为:y=x2-2x-3;
(2)∵y=x2-2x-3;
=(x-1)2-4,
∴该抛物线的顶点坐标为:(1,-4).
(3)∵图象经过:(-1,0),对称轴为:x=1,
∴图象与x轴另一交点坐标为:(3,0),
∴当x<-1或x>3时,y>0,-1<x<3时,y<0;
(4)存在,
∵S△PAB=8,AB=4,
∴P点纵坐标为4,
∴4=x2-2x-3;
解得:x1=1-2
,x2=1+2
,
∴P1(1-2
,4),P2(1+2
,4).
 解:(1)∵抛物线y=x2+bx+c的部分图象可得:
解:(1)∵抛物线y=x2+bx+c的部分图象可得:图象经过:(-1,0),对称轴为:x=1,
∴
|
解得:
|
∴该抛物线的表达式为:y=x2-2x-3;
(2)∵y=x2-2x-3;
=(x-1)2-4,
∴该抛物线的顶点坐标为:(1,-4).
(3)∵图象经过:(-1,0),对称轴为:x=1,
∴图象与x轴另一交点坐标为:(3,0),
∴当x<-1或x>3时,y>0,-1<x<3时,y<0;
(4)存在,
∵S△PAB=8,AB=4,
∴P点纵坐标为4,
∴4=x2-2x-3;
解得:x1=1-2
| 2 |
| 2 |
∴P1(1-2
| 2 |
| 2 |
点评:此题主要考查了二次函数的综合应用,利用图象上点的坐标求出解析式进而利用图象得出x取何值时y的符号,此题是中考中重点题型,同学们应重点掌握.

练习册系列答案
相关题目
 (2009•裕华区一模)如图甲、乙二人沿相同的路线由A到B匀速行进,A、B两地间的路程为20km,他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示据图象信息可知,乙出发
(2009•裕华区一模)如图甲、乙二人沿相同的路线由A到B匀速行进,A、B两地间的路程为20km,他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示据图象信息可知,乙出发