��Ŀ����
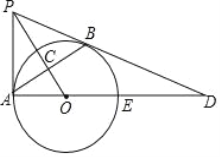
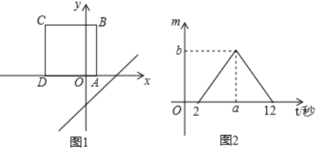
����Ŀ����ͼ��������A��B�����Ӧ���������ֱ�Ϊa��b����a��b����|a+4|+��2b��12��2��0��
![]()
��1����a��b��ֵ��
��2����C��������һ�㣬���Ӧ������x��
������C�ڵ�A��B֮�䣬����|x+4|��|x��6|��
����CB��2CA����x��ֵ��
��3����M�͵�N�ֱ�ͬʱ�ӵ�O�͵�A�������ֱ���ÿ��2����λ���ȣ�ÿ��3����λ���ȵ��ٶ��������������˶������ͬʱ����T��ÿ��5����λ���ȵ��ٶȴӵ�B��������ʼ�����˶���������M���������������˶���������N���������������˶������M���������������أ����������ֱ��M��N��������ʱ����Tֹͣ�˶������T�˶���·��һ���Ƕ��ٸ���λ���ȣ���Tֹͣ��λ������Ӧ�����Ƕ��٣�
���𰸡���1��a����4��b��6����2����2x��2����x����14����3��20��8.
��������
��1�����ݷǸ��������ʿ����a��b��ֵ��
��2�����ɣ�1���ó�x��ȡֵ��Χ���ٸ��ݾ���ֵ�����ʽ��л�����㣻��������֪����C�������ڵ�B���Ҳ࣬�ֱ�����C��AB֮���C��A���ʱ���з�����⣻
��3����M��N��������ʱ�˶�ʱ��Ϊt�룬��������ʱ����ٶȲ�=��ʼ���룬�г����̿��������ʱ�䣬����T���˶��ٶȳ���ʱ��õ�·�̣�����M��N��T��ͬһ�㣬���M��λ������Ӧ�ĵ�������.
�⣺��1����|a+4|+��2b��12��2��0��
��a+4��0��2b��12��0��
��a����4��b��6��
��2���١ߵ�C�ڵ�A��B֮�䣬
�ੁ4��x��6��
��x+4��0��x��6��0��
|x+4|��|x��6|��x+4����6��x����2x��2��
��������֪����C�������ڵ�B���Ҳ࣬
��BC�ij���Ϊ6��x��AC��|x+4|��
��x����4ʱ��6��x��2��x+4����
��ã�x����![]() ��
��
��x����4ʱ��6��x��2����4��x����
��ã�x����14��
��3����M��N��������ʱ�˶�ʱ��Ϊt�룬
��3t��2t��4��
��t��4��
��T�˶���·��Ϊ��4��5��20��
��ʱM��N��T��ͬһ�㣬
���T��λ������Ӧ����Ϊ��2��4��8��

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�