Question

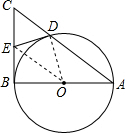
在Rt△ABC中，直角边AB为直径的半圆O，与斜边AC交于D，点E是BC边的中点，连接DE，
①DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明情况．
②若AC、AB的长是方程x²-10x+24=0的根，求直角边BC的长．

Answer 1

解：（1）DE与半圆O相切．
证明：连接OD、OE．
∵O、E分别是BA、BC的中点，
∴OE∥AC，
∴∠BOE=∠BAC，∠EOD=∠ADO，
∵OA=OD，
∴∠ADO=∠BAC．
∴∠BOE=∠EOD．
∵OD=OB，OE=OE，
∴△OBE≌△ODE．
∴∠ODE=∠OBE=90°．
∴DE与半圆O相切．

（2）∵AC，AB的长是方程x²-10x+24=0的两个根，
∴解方程x²-10x+24=0得：x₁=4，x₂=6．
∵AB＜AC，
∴AB=4，AC=6，
∴BC====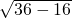2．
分析：①相切．连接OD，证明OD⊥DE即可．连接OE，则OE∥AC，可证∠BOE=∠DOE，根据SAS判定△BOE≌△DOE，得∠ODE=∠B=90°．得证．
②解方程可得AC、AB的长，运用勾股定理求BC．
点评：此题考查了相似三角形的判定和性质的应用、切线的判定、解一元二次方程、勾股定理等知识点，综合性较强．