题目内容
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
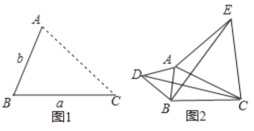
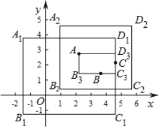
如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.
(1)已知A(﹣2,3),B(5,0),C(t,﹣2).
①当t=2时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,求直线AC的表达式;
(2)已知点D(1,1).E(m,n)是函数y=![]() (x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
(x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
【答案】(1)35,![]() ;(2)
;(2)![]() .
.![]()
【解析】
(1)①由矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形,得出最优覆盖矩形的长为:2+5=7,宽为3+2=5,即可得出结果;
②由定义可知,t=-3或6,即点C坐标为(-3,-2)或(6,-2),设AC表达式为y=kx+b,代入即可求出结果;
(2)OD所在的直线交双曲线于点E,矩形OFEG是点O,D,E的一个面积最小的最优覆盖矩形,OD所在的直线表达式为y=x,得出点E的坐标为(2,2),⊙P的半径最小r=![]() ,当点E的纵坐标为1时,⊙P的半径最大r=
,当点E的纵坐标为1时,⊙P的半径最大r=![]() ,即可得出结果.
,即可得出结果.
(1)①∵A(﹣2,3),B(5,0),C(2,﹣2),矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形,
∴最优覆盖矩形的长为:2+5=7,宽为3+2=5,
∴最优覆盖矩形的面积为:7×5=35;
②∵点A,B,C的最优覆盖矩形的面积为40,
∴由定义可知,t=﹣3或6,即点C坐标为(﹣3,﹣2)或(6,﹣2),
设AC表达式为y=kx+b,
∴![]() 或
或![]()
∴![]() 或
或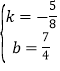
∴y=5x+13或![]() ;
;
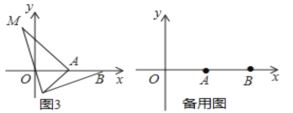
(2)①OD所在的直线交双曲线于点E,矩形OFEG是点O,D,E的一个面积最小的最优覆盖矩形,如图1所示:
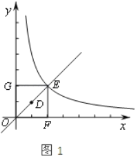
∵点D(1,1),
∴OD所在的直线表达式为y=x,
∴点E的坐标为(2,2),
∴OE=![]() ,
,
∴⊙P的半径最小r=![]() ,
,
②当DE∥x轴时,即:点E的纵坐标为1,如图2所示:
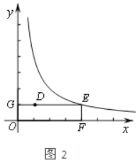
∵点D(1,1).E(m,n)是函数y=![]() (x>0)的图象上一点
(x>0)的图象上一点
∴1=![]() ,解得x=4,
,解得x=4,
∴OE═![]() =
=![]() ,
,
∴⊙P的半径最大r=![]() ,
,
∴![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】已知y是x的函数,自变量x的取值范围是x≠0的全体实数,如表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … |
|
| ﹣ | ﹣ | ﹣ |
|
|
| m |
| … |
小华根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
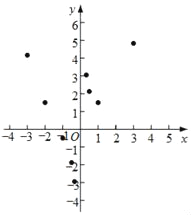
(1)从表格中读出,当自变量是﹣2时,函数值是 ;
(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(3)在画出的函数图象上标出x=2时所对应的点,并写出m= .
(4)结合函数的图象,写出该函数的一条性质: .