题目内容
(2012•佛山)(1)按语句作图并回答:
作线段AC(AC=4),以A为圆心a为半径作圆,再以C为圆心b为半径作圆(a<4,b<4,圆A与圆C交于B、D两点),连接AB、BC、CD、DA.
若能作出满足要求的四边形ABCD,则a、b应满足什么条件?
(2)若a=2,b=3,求四边形ABCD的面积.
作线段AC(AC=4),以A为圆心a为半径作圆,再以C为圆心b为半径作圆(a<4,b<4,圆A与圆C交于B、D两点),连接AB、BC、CD、DA.
若能作出满足要求的四边形ABCD,则a、b应满足什么条件?
(2)若a=2,b=3,求四边形ABCD的面积.
分析:(1)根据题意画出图形,只有两圆相交,才能得出四边形,即可得出答案;
(2)连接BD,根据相交两圆的性质得出DB⊥AC,BE=DE,设CE=a,则AE=4-a,根据勾股定理得出关于a的方程,求出a,根据三角形的面积公式求出即可.
(2)连接BD,根据相交两圆的性质得出DB⊥AC,BE=DE,设CE=a,则AE=4-a,根据勾股定理得出关于a的方程,求出a,根据三角形的面积公式求出即可.
解答:(1)解: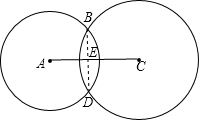
能作出满足要求的四边形ABCD,则a、b应满足的条件是a<4,b<4,4<a+b<8且|a-b|<4.
(2)解:连接BD,交AC于E,
∵⊙A与⊙C交于B、D,
∴AC⊥DB,BE=DE,
设CE=x,则AE=4-x,
∵由勾股定理得:BE2=32-x2=22-(4-x)2,
解得:x=
,
∴BE=
=
,
则四边形ABCD的面积是2×
×AC×BE=4×
=
,
答:四边形ABCD的面积是
.

能作出满足要求的四边形ABCD,则a、b应满足的条件是a<4,b<4,4<a+b<8且|a-b|<4.
(2)解:连接BD,交AC于E,
∵⊙A与⊙C交于B、D,
∴AC⊥DB,BE=DE,
设CE=x,则AE=4-x,
∵由勾股定理得:BE2=32-x2=22-(4-x)2,
解得:x=
| 21 |
| 8 |
∴BE=
32-(
|
3
| ||
| 8 |
则四边形ABCD的面积是2×
| 1 |
| 2 |
3
| ||
| 8 |
3
| ||
| 2 |
答:四边形ABCD的面积是
3
| ||
| 2 |
点评:本题考查了作图-复杂作图,相交两圆的性质,勾股定理的应用,通过做此题培养了学生的动手操作能力和计算能力,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
相关题目
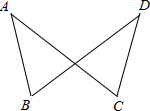 (2012•佛山)如图,已知AB=DC,DB=AC
(2012•佛山)如图,已知AB=DC,DB=AC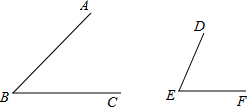 (2012•佛山)比较两个角的大小,有以下两种方法(规则)
(2012•佛山)比较两个角的大小,有以下两种方法(规则) (2012•佛山)如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
(2012•佛山)如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )