题目内容
如图,已知△ABC与△ACD都是直角三角形,∠B=∠ACD=90°,AB=4,BC=3,CD=12.则△ABC的内切圆与△ACD的内切圆的位置关系是( )


| A.内切 | B.相交 | C.外切 | D.外离 |
C
试题分析:首先求出AC、AD的长,进而求出两内切圆的半径,以及四边形RBQS和四边形MCFN是正方形,得出两圆与AC切于同一点,即可得出答案.
作出两圆的内切圆,设且点分别为R,Q,T,以及M,F

∵∠B=∠ACD=90°,AB=4,BC=3,CD=12,

∴直角三角形△ABC与△ACD的内切圆半径分别为:
 ,
, ,
,可得四边形RBQS和四边形MCFN是正方形,
则RQ=RS=BQ=SQ=1,FC=NF=CM=MN=2,
∴QC=3-1=2,设⊙S与AC切于点T,则CT=2,
∵CM=CT=2,
∴T与M重合,即两圆与AC切于同一点.
故△ABC的内切圆与△ACD的内切圆的位置关系是外切.
故选C.
点评:熟记直角三角形的内切圆半径求法,根据已知得出两圆与AC切于同一点是解题关键.

练习册系列答案
相关题目


 是Rt
是Rt ABC的外接圆,
ABC的外接圆, ABC=90
ABC=90 ,点P是
,点P是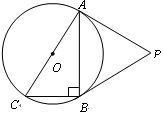
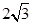 ,BC=2,求
,BC=2,求 中,半径长
中,半径长 ,
, ;以
;以 为直径作半圆
为直径作半圆 ,点
,点 是弧
是弧 上的一个动点,
上的一个动点, 与半圆
与半圆 ,
, ⊥
⊥ ,
, 交于点
交于点 ,连结
,连结 .
.
 ;
; ,
,  ,试求
,试求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 上,当
上,当 ∽
∽ 的长度.
的长度. 


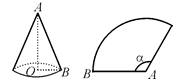
 的弦,半径OA=2,
的弦,半径OA=2, ,则弦AB的长为( )
,则弦AB的长为( )


