题目内容
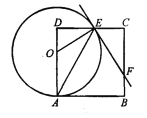
【题目】如图,点O在边长为8的正方形ABCD的AD边上运动(4<C)A<8),以O为圆心,OA长为半径作圆,交CD于点E,连接OE、AE,过点E作直线EF交BC于 点F,且∠CEF=2∠DAE.
(1)求证:直线EF为⊙O的切线;
(2)在点O的运动过程中,设DE=x,解决下列问题:
①求OD·CF的最大值,并求此时半径的长;
②试猜想并证明△CEF的周长为定值.
【答案】(1)证明见解析;(2)16,5;证明见解析.
【解析】
试题分析:(1)由OA=OB得∠OAE=∠OEA,则根据三角形外角性质得∠DOE=2∠DAE,由于∠CEF=2∠DAE,则∠CEF=∠DOE,加上∠DOE+∠DEO=90°,则∠CEF+∠DEO=90°,所以∠OEF=90°,于是可根据切线的判定定理得到直线EF为⊙O的切线;
(2)由于∠CEF=∠DOE,根据三角形相似的判定得到Rt△DOE∽Rt△CEF,利用相似比得ODCF=DEEC=x(8-x),配方得ODCF=-(x-4)2+16,然后根据二次函数的性质得当x=4时,ODCF的值最大,最大值为16;设此时半径为R,则OA=OE=R,OD=8-R,在Rt△ODE中,根据勾股定理可计算出此时半径为5;
(3)在Rt△ODE中,利用勾股定理得到(8-OE)2+x2=OE2,则OE=4+![]() ,OD=8-OE=4-
,OD=8-OE=4-![]() ,再利用Rt△DOE∽Rt△CEF得到相似比
,再利用Rt△DOE∽Rt△CEF得到相似比![]() ,即
,即 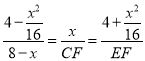 ,可计算得CF=
,可计算得CF=![]() ,EF=
,EF=![]() ,然后根据三角形周长的定义得到△CEF的周长得到CE+CF+EF=8-x+
,然后根据三角形周长的定义得到△CEF的周长得到CE+CF+EF=8-x+![]() +
+![]() ,再进行分式的化简运算即可得到△CEF的周长为16.
,再进行分式的化简运算即可得到△CEF的周长为16.
试题解析:(1)证明:∵OA=OB,
∴∠OAE=∠OEA,
∴∠DOE=2∠DAE,
∵∠CEF=2∠DAE,
∴∠CEF=∠DOE,
∵四边形ABCD为正方形,
∴∠D=90°,
∴∠DOE+∠DEO=90°,
∴∠CEF+∠DEO=90°,
∴∠OEF=90°,
∴OE⊥EF,
∴直线EF为⊙O的切线;
(2)解:∵∠CEF=∠DOE,
∴Rt△DOE∽Rt△CEF,
∴![]() ,
,
∴ODCF=DEEC,
∵DE=x,
∴EC=8-x,
∴ODCF=x(8-x)
=-x2+8x
=-(x-4)2+16,
当x=4时,ODCF的值最大,最大值为16,
设此时半径为R,则OA=OE=R,OD=8-R,
在Rt△ODE中,
∵OD2+DE2=OE2,
∴(8-R)2+42=R2,解得R=5,
即此时半径为5;
(3)猜想△CEF的周长为16.
在Rt△ODE中,OD2+DE2=OE2,即(8-OE)2+x2=OE2,
∴OE=4+![]() ,
,
∴OD=8-OE=4-![]() ,
,
∵Rt△DOE∽Rt△CEF,
∴![]() ,即
,即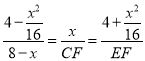
∴CF=![]() ,EF=
,EF=![]() ,
,
∴△CEF的周长=CE+CF+EF= CE+CF+EF=8-x+![]() +
+![]() =16.
=16.